Introduction - Logic and Logical Form
What is the subject matter of logic?
Being logical entails using only valid arguments when reasoning or arguing. Logic constitutes the scientific study of valid arguments.
Every argument comprises premises and a conclusion. Both premises and the conclusion are sentences. Here are two examples:
| Bob is not sick with the flu because if he were, he would have a fever, and he doesn’t. |
| If Bob is sick with the flu, he will have a fever. He has a fever. Therefore, he is sick with the flu. |
Both arguments have two premises. When analyzing an argument, we will often list its premises one below the other, and below them, separated by a line, we will state the conclusion:
| If Bob is sick with the flu, he has a fever. |
| Bob does not have a fever. |
| Bob is not sick with the flu. |
| If Bob is sick with the flu, he has a fever. |
| Bob has a fever. |
| Bob is sick with the flu. |
An argument is valid when it is impossible for the conclusion to be false if the premises are true. Otherwise, it is invalid. The first of the above arguments is valid because if its premises are true, its conclusion cannot be false. The second argument is invalid because (assuming that the first premise is true) it is possible for Bob to have a fever and not be sick with the flu; he may be ill with something else. In this case, the premises will be true, and the conclusion will be false. The first argument is an example of a logically valid inference, and the second of a logically invalid one.
Logical inference and logical form
An inference is logically valid if it is logically impossible for the conclusion to be false when the premises are true. Instead of stating that an inference is logically valid, we may say that the premises logically entail the conclusion, or that the conclusion logically follows from the premises, or that it is a logical consequence of the premises, etc. The relation of logical inference between sentences is of fundamental interest to logic, so an important question is whether there are universal procedures through which we can always determine whether a certain sentence can be validly inferred from certain premises. Another important question is whether there are universal procedures by which, if a sentence logically follows from certain premises, we can prove that this is the case. Without being one and the same question, these questions are related and are not at all trivial. Modern logic gives a negative answer to the first – there is no universal recipe through which it can always be determined whether a sentence logically follows from certain premises. However, the second question has an affirmative answer – there are universal proof procedures through which, if a sentence is а logical consequence of certain premises, this can be demonstrated.
The premises and conclusion of each inference (argument) are sentences that can be (and are) true or false. We will refer to such sentences as statements or propositions. Among the sentences below, only the last one is a statement.
Is it Tuesday tomorrow?
Say what you think without worrying.
If only I were ten years younger!
All mushrooms are plants.
Questions, orders, requests, exclamations, etc., are sentences, but they are not statements because they are not true or false.
It is important to distinguish between the logical validity or invalidity of an inference and the truth or falsity of the sentences it comprises. Whether a sentence is a logical consequence of certain premises has (almost) nothing to do with the truth or falsity of the sentence or the premises. Consider the following two inferences:
| All winged creatures are gods. |
| All humans have wings. |
| All humans are gods. |
| All predators are animals. |
| All tigers are animals. |
| All tigers are predators. |
All three sentences in the first inference are false, and all three in the second are true. However, the first is logically valid, while the second is not. Whoever would make the first inference would be more logical than whoever would make the second, although the world in which the first person thinks they live would be much farther from reality than the world of the second, less logical person. What makes the first inference logically valid is that if the premises were true, the conclusion would be (necessarily) also true. It is impossible for the conclusion to be false if the premises are true, which, as we noted above, is the criterion for logical validity. In contrast, while all sentences in the second inference are true, it is not logically impossible for the conclusion to be false when both premises are true, because it is not logically impossible for tigers and predators to be animals without tigers being predators. The diagram below shows why such a situation (though not real) is possible.
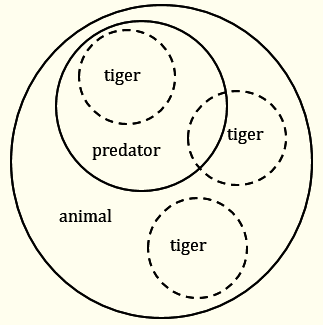
The circles in the diagram are related to the corresponding sets of things. For example, the circle of predators being fully included in the circle of animals corresponds to a state of affairs in which the set of predators is a subset of the set of animals, i.e., in which all predators are animals (the first premise). The circle of predators and the circle of tigers being included in the circle of animals corresponds to the assumption that the premises ("All predators are animals" and "All tigers are animals") are true. Under this assumption, the circle of tigers has three possible positions relative to the circle of predators – it could be fully included in it (the actual situation), only partially included, or completely excluded. The second and the third possibilities make the conclusion ("All tigers are predators") false while preserving the truth of the premises. This shows that it is (logically) possible for the conclusion to be false if the premises are true, which means that the inference is invalid – it does not guarantee the truth of the conclusion when the premises are true.
In contrast, the diagram below shows that if the premises of the first inference were true, the conclusion could not be false.
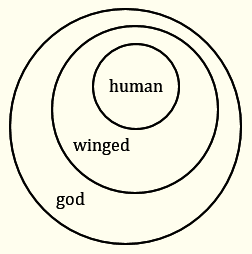
If the premises ("All winged creatures are gods" and "All humans have wings") were true, the circle of winged creatures would have to be fully included in the circle of gods, and the circle of humans would have to be fully included in the circle of winged creatures (as is in the diagram). But then the circle of humans would have to be fully included in the circle of gods – i.e., there is no way for the conclusion to be false if the premises are true. This shows that the inference is logically valid even though the sentences are in fact false. Logic is beyond the actual situation – it takes into account every possible world.
The logical validity or invalidity of an inference is determined by its structure, not by what the sentences are talking about – the form, not the content, is logically important. No matter how we change the content of the above two inferences, if we preserve their structure (i.e., preserve their logical form), the first will continue to be logically valid and the second logically invalid. For example, the inferences below are obtained from the above by replacing words or expressions in them but leaving their overall structures unchanged. As a result, the subjects are changed completely, but the logical forms of the inferences are preserved:
| All who have ever forgotten their umbrellas at my place are men. |
| All my friends born in March have forgotten their umbrellas at my place. |
| All my friends born in March are men. |
| All squirrels are mammals. |
| All elephants are mammals. |
| All elephants are squirrels. |
The first inference is obtained from the first example above by replacing "winged creatures" with "those who have ever forgotten their umbrellas at my place", "gods" with "men", and "humans" with "my friends born in March", and the second is obtained from the second example above by replacing "predators" with "squirrels", "animals" with "mammals", and "tigers" with "elephants". As a result, each of the three false sentences in the first inference above has become a sentence that could be true or false (depending on who and when is speaking), and the premises of the second example continue to be true, but the conclusion has become false. The point is that all these changes do not affect the validity or invalidity of the inferences – the first continues to be valid, and the second invalid, for the same reasons indicated in the diagrams above.
Because logical validity or invalidity of inferences is determined by their form, not by their content, in logic, we use symbols to replace the content words or expressions so that the logical form stands out. We may explicate the logical forms of the above four inferences by replacing the content expressions in them with "S", "M", and "P". Then the two valid inferences will have the form:
| All M are P. |
| All S are M. |
| All S are P. |
and the two invalid will have the form
| All P are M. |
| All S are M. |
| All S are P. |
Accordingly, the diagrams below show that every inference having the first form is logically valid and every inference having the second form is logically invalid.


Let me emphasize again: whether an inference is logically valid is determined neither by the content of the statements involved nor by whether they are true or false; it is determined by the logical form of the inference. So, although there is a connection between logical validity and truth, being logical and telling the truth are different things. One may make only logically valid inferences but if they start from false premises, they may come to a false conclusion; and vice versa – although one may make invalid inferences, they may start from true premises and (by chance) come to a true conclusion. What logical validity guarantees is that if the premises are true, the conclusion will also be true. So, the ideal case is to start from true premises and make only logically valid inferences. Then we will have the strongest possible guarantee – the logical one – that our conclusions will be true.
Logical words
If what determines whether an inference is logically valid or not is its logical form, what determines the logical form itself? The logical form of an inference is determined by the logical forms of the sentences (the premises and the conclusion) it consists of, and the logical forms of the latter are determined by words or expressions in them that we may call logical. Such words are "all" and "are". Above, we made explicit the logical form of some inferences that contain these two words by replacing the other, non-logical words with symbols ("S", "M", and "P"). As a result, we obtained two inference schemes:
| All M are P. | All P are M. | |
| All S are M. | All S are M. | |
| All S are P. | All S are P. |
No matter what words or phrases we substitute for the symbols "S", "M", and "P" (the same expression for the same symbol), from the first scheme we will always obtain logically valid inferences, and from the second scheme, we will always form logically invalid inferences.
The situation is the same with the examples of a valid and invalid inference we started with:
| If Bob is sick with the flu, he will have a fever. |
| Bob does not have a fever. |
| Bob is not sick with the flu. |
| If Bob is sick with the flu, he will have a fever. |
| Bob has a fever. |
| Bob is sick with the flu. |
Their logical form is determined by the logical words "if..., then..." and "not". By replacing the other (non-logical) expressions, which in this case are whole sentences, with symbols, we obtain the following inference schemes:
| If A, then B. | If A, then B. | |
| not-B. | B | |
| not-A. | A |
Every inference that has the form of the first scheme (i.e., obtained by replacing "A" and "B" with sentences) will be logically valid, and every inference that has the form of the second will be logically invalid.
Here are some examples of logical words and expressions:
| "every" "any" "each" "some" "a" (indefinite article) "the" "not" "no" "is" "are" "exist" "there is" "and" "but" "or" "if …, then …" "only if" "neither … nor …" "unless" "identical" "other" "necessary" "possible" … |
Logical words occur in every area and context. Since the validity or invalidity of inferences depends on the logical form, and the logical form is determined by the logical words, ultimately, whether a person is logical or not depends on how they use logical words; it does not depend on the content of the statements made. If a person is logical, they will be so regardless of whether they are engaged in politics, philosophy, biology, etc. (Similarly, if a person is not logical).
A brief history of logic
Aristotle (4th century BC) is the founder of logic as a science. At the center of his logical theory are the so-called syllogisms – a kind of inference that involves logical words such as "all", "some", "none", etc. Most of the examples used above were syllogisms. An example is as follows:
| All winged creatures are gods. |
| All humans have wings. |
| All humans are gods. |
Aristotle’s logical writings were called Organon, which means "instrument". The Organon includes the books Categories, Topics, On Interpretation, Prior Analytics, and Posterior Analytics.
Aristotle formulated two principles that he considered the basis of any theoretical activity: the law of non-contradiction and the law of excluded middle. According to the first, a statement and its negation cannot both be true, and according to the second, at least one of them must be true. For example, although we do not know if the sentence "There is extraterrestrial life" is true, by the law of non-contradiction we know that the sentences "There is extraterrestrial life" and "There is no extraterrestrial life" cannot both be true, and by the law of excluded middle we know that at least one of them is true (they cannot both be false).
Aristotle’s logical theory had a huge influence on Western thought. Essentially, it constituted the entirety of the Western world's logic from the end of Antiquity until the late 19th century when modern logic emerged.
Megarian-Stoic logic originated with Euclid of Megara (5th – 4th century BC), a pupil of Socrates. His students were called "Megarians" and later "Dialecticians". By "dialectic," the ancient Greeks understood the exchange of arguments between the supporters of a thesis and its opposite (antithesis), which could result in the rejection of one of them or in a kind of combination (synthesis) of them. Notable figures among the Megarians were Diodorus Cronus (4th – 3rd century BC) and his student Philo (4th – 3rd century BC).
Later (3rd century BC), the logical views of the Megarians were adopted and systematized by the Stoics, hence the name "Megarian-Stoic logic". The most notable logician among the Stoics was Chrysippus (3rd century BC), who wrote over 300 logical works, none of which survived.
Among other things, Megarian-Stoic logicians were interested in the concepts of necessity and possibility. For example, Diodorus insisted that "the impossible cannot follow from the possible," and Chrysippus denied that. (Today, modal logic deals with the concepts of necessity and possibility.) They were also interested in when a conditional sentence ("If p, then q") is true. Philo thought that to be true it is enough that it is not true that p is true and q is false, while Diodorus argued that to be true it must be impossible that p is true and q is false. (The first view corresponds to the modern understanding of material implication (or conditional) and the second to that of strict implication.) Generally, a striking difference between Megarian-Stoic logic and Aristotle’s logic is that the representatives of the former were interested in the logical words through which sentences are connected in more complex sentences, such as "if ..., then ...", while Aristotle’s logic completely ignored them. (Today, propositional logic deals with these logical words.) Another thing Megarian-Stoic logicians were interested in was the notion of meaning. The Stoics, for example, thought that what is expressed by a sentence (not the object or objects it is talking about, but its very meaning) is real. (Today, such abstract entities corresponding to meanings of sentences are often called "propositions"1. It is another matter that many philosophers do not believe they exist.)
For centuries, Megarian-Stoic logic was the dominant logical tradition in the ancient world. After the end of the Roman Empire (5th century), no original works of Megarian-Stoic logic survived. Aristotle’s logic was more fortunate.
During the so-called "Dark Ages" (5th – 10th century), one of the few connections to the logic of the ancient Greeks was the Christian philosopher Boethius (5th – 6th century), who was familiar with some of Aristotle’s writings. Until the 12th century, the only available logical works of Aristotle in the Western world were Categories and On Interpretation. In the early 13th century, the rest of The Organon (Prior and Posterior Analytics and Topics) was discovered, which resulted in the so-called scholastic logic, a refined form of Aristotelian logic that further developed it but only in the details.
In a broader sense, the term "traditional logic" refers to Aristotle’s logic as opposed to modern logic. In the narrower sense, it refers to a characteristic of the early modern period psychologized version of Aristotle’s logic, the beginning of which is a textbook written in the late 17th century – Logic or the Art of Thinking (1662) by Antoine Arnauld and Pierre Nicole, which became known as the Port-Royal Logic. Port Royal is a monastery in France that was the center of the theological movement of Jansenism, of which the two authors were prominent representatives. They were influenced by Descartes’ philosophical views. The textbook gained immense popularity and became the standard textbook on logic in France and England in the 17th and 18th centuries. As logical content, traditional logic (in the narrow sense) follows Aristotle’s logic but psychologizes it. While Aristotle and the scholastic tradition relate logic to arguments and sentences – i.e., to language, traditional logic relates it to ideas and thoughts as acts of the mind. For traditional logic, logical form is not a form of language, it is a form of thinking. For example, instead of the word "man", in traditional logic one would talk of the concept of man; instead of the sentence "All humans are mortal" – of the judgement that all humans are mortal; instead of inferences expressed in language – of reasonings as actions of the human mind, etc. In its extreme, such an approach regards logic as subordinate to psychology and is called "psychologism" (a term with a negative connotation).
With the emergence of modern logic, this psychologizing of logic ended. The contemporary understanding of logic connects it with language even more than Aristotle – arguments, inferences, proofs etc. are considered sequences of sentences (i.e., linguistic entities) whose logical validity or invalidity is determined, in the end, by certain logical words.
Modern logic
In the late 19th and early 20th centuries, modern logic emerged. Its classical variant is called predicate logic or first-order logic. The resources for logical analysis of predicate logic are much greater than those of (Aristotle’s) traditional logic. A part of it, propositional logic, treats the inferences whose logical validity or invalidity depends on the so-called logical connectives – logical words (such as "and", "or", "if ..., then ...", etc.) that connect sentences in more complex, compound sentences. In the scope of propositional logic are, for example, the above-mentioned inference schemes
| If A, then B. | If A, then B. | |
| not-B. | B | |
| not-A. | A |
Beyond the scope of propositional logic but within that of predicate logic (which, as mentioned, contains propositional logic as a part) are inferences whose logical validity depends on logical words such as "some", "all", "none", "exist", etc. Such inferences are the subject of traditional (Aristotelian) logic but the syllogisms, which the latter mostly deals with, are only a small (though important) part of them. There are many other inferences (including some syllogisms) that traditional logic, unlike predicate logic, cannot properly analyze.
Predicate and propositional logic (the latter being part of the former) are the classical modern logic. In addition, there are extensions and alternatives to them sometimes referred to as non-classical logics. Such is the group of modal logics, which are extensions of classical logic derived from it by adding to its symbolic language the so-called modal operators. The latter are symbolic equivalents to such (supposedly logical) words as "necessary", "possible", "permitted", "obligatory", and others. Modal logics differ in what those words are. In alethic modal logic, the modal operators correspond to "necessary" and "possible"; in deontic modal logic to "obligatory" and "permitted"; in temporal modal logic to such related to time expressions as "it always was" and "it will be"; in the epistemic modal logic to words like "knows" and "believes".
Modal logics are an attempt to extend classical logic because they accept its principles and try to extend its scope. In addition, there are alternatives to classical logic, which reject some of its principles, replacing them with others. Such is, for example, three-valued logic, which rejects the principle of bivalence according to which every statement is true or false. Three-valued logic assumes that some statements are neither true nor false, but have a third truth value – for example, undetermined or meaningless.
1. The sense in which we use this word here is different. For us "proposition" means a statement (a kind of sentence), not an extra-linguistic entity denoted by a sentence. ↩

