2.6 Venn diagrams
Venn diagrams were invented at the end of the 19th century (Venn, 1880) and are located somewhere in the intermediate territory between traditional and modern logic, so to speak. On the one hand, they serve to determine the logical validity of inferences composed exclusively from categorical sentences (mostly syllogisms) but, on the other hand, the categorical sentences themselves are analyzed in the same way as contemporary, rather than traditional, logic does.
I have mentioned many times that traditional logic assumes that the extensions of the terms of categorical sentences are not empty. This is correct for particular affirmative sentences since an I-sentence may be paraphrased with the sentence “There exists at least one S that is a P”, which is committed to the existence of at least one S and the existence of at least one P. In addition, a particular negative sentence is committed to the existence of at least one S without committing itself to the existence of a P since it can be paraphrased as “There exists at least one S that is not a P”. Thus far, traditional and contemporary logic are not in disagreement. The difference is that for contemporary logic there is no other way to express an existential commitment by a categorical sentence, while for traditional logic the extensions of S and P are never empty – we are always committed to the existence of at least one S and the existence of at least one P. The reason is the immediate inference of subalternation. For traditional logic, universal sentences entail (by subalternation) the particular sentences with the same quality and the same subject and predicate – A entails I, and E entails O. It follows that A-sentences must imply that there exist at least one S and at least one P, and E-sentences must imply that there exist at least one S. Otherwise, I-sentences will be false if there are no S or P, while the corresponding A-sentences could be true; similarly for O and E-sentences if there are no S. A sentence cannot logically entail a sentence if it is possible the former to be true while the latter is false. So far, we have that traditional logic assumes that the extensions of the subjects and the predicates of the two affirmative sentences (A and I) and of the subjects of the two negative sentences (E and O) are not empty. However, because of the immediate inference of conversion, also the extensions of the predicates of the E-sentences cannot be empty. Еach E-sentence implies by conversion an E-sentence in which the predicate of the former has become a subject, and the subject of an E-sentence (as we saw) is never empty. Such inference would not be valid if the extension of predicate of the first sentence could be empty, and the first sentence was any E-sentence. Therefore, also the extension of the predicate of an E-sentence cannot be empty in traditional logic. It remains to show that the extension of the predicate of an O-sentence cannot be empty. This is evident from the following. Uttering an arbitrary O-sentence, the E-sentence with the same subject and predicate will be true or false. If true, the extension of its predicate will not be empty (we have already seen that), and therefore the extension of the predicate of the O-sentence, which is the same term, will not be empty. If the E-sentence is false, then the contradictory I-sentence will be true, so the extension of its predicate will not be empty, and therefore the extension of the predicate of the O-sentence, which is the same term, will not be empty. It is not empty in either case. Thus, we have shown that, in order to be consistent, traditional logic has to assume that the extensions of the subject and the predicate of a categorical sentence are never empty.
We have already said that for modern logic (and, as we will see, in a Venn diagram) only the sentences that are particular in quantity commit themselves to the existence of things that are S or P (things that fall under their subject or predicate). More specifically, an I-sentence is committed to the existence of at least one S and at least one P, and an O-sentence is committed to the existence of at least one S remaining noncommittal to the existence of a P. The universal affirmative (A) and the universal negative (E) sentences do not contain any information about the existence of S’s or P’s and are trivially true when there are no S. The reason for this is that each A-sentence “All S are P” is considered synonymous with the sentence “If a thing is an S, then it is a P” and each E-sentence “No S are P” is considered synonymous with “If a thing is an S, then it is not a P”. The latter synonymous sentences are trivially true when there is no an S, whether or not there is a P.
This difference between modern and traditional logic in the treatment of categorical sentences leads to significant differences in the treatment of the square of opposition, the immediate inference of conversion, and what syllogisms are considered valid, which we will discuss below.
Now let us see what a Venn diagram is. The following four diagrams correspond to the four categorical sentences:

Each term (the subject S and predicate P) has its own circle. The position of the circles is fixed as shown. The interior of each circle corresponds to the things that fall under the term, and the space outside the circle corresponds to things that do not fall under the term. In this way, in each of the four diagrams there are four regions, corresponding to four classes (some of them possibly empty). The lens-like common part of the circles of S and of P corresponds to things that are both S and P. The space outside both circles corresponds to the things that are neither S nor P. The left-hand segment of the circle of S corresponds to the things that are S but not P. The right-hand segment of the circle of P corresponds to the things that are P but not S. Each of the regions can be marked in two possible ways: either by shading (in our case coloring in gray) or by putting an “x” in it. Shading a region means that the corresponding class is empty. Putting an “x” in a region means that the corresponding class is not empty. Lack of shading or “x” means lack of information (we do not know whether the class is empty or not).
In the diagram on the upper left, the region of the things that are S but not P is marked as empty. In this way the diagram expresses that there are no S that are not P, i.e. if a thing is an S, it is a P (“All S are P”). This is how a universal affirmative (A) sentence is expressed through a Venn diagram.
In the upper right diagram, the region of the things that are both S and P is marked as empty. Thus, the diagram tells us that there are no S that are P, i.e. if a thing is an S, it is not a P (“No S are P”). This is how a Venn diagram expresses a universal negative (E) sentence.
In the lower left diagram, there is an “x” in the region of the things that are both S and P. As “x” means existence, the diagram tells us that there is at least one S that is a P (“Some S are P”). This is how a particular affirmative (I) sentence is expressed by a Venn diagram.
The diagram at bottom right contains the information that the class of all things that are S but not P is not empty, i.e. there is at least one S that is not a P (“Some S are not P”). This is how a particular negative (O) sentence is expressed through a Venn diagram.
The diagrams of the universal affirmative (A) and the universal negative (E) sentences (the above two) do not contain information about the existence of anything. The only way to express existence in a Venn diagram is to put “x” in a region. The absence of “x” (together with the lack of shading) does not mean that the region is empty, but that there is no information. As a result, both diagrams allow each of the four possible cases concerning S and P – the extensions of both terms to be empty (the case when there are neither an S nor a P), both not to be empty (there is an S and a P), one is empty and the other is not (there is an S but not a P, and vice versa). What the first diagram does not allow (by shading the corresponding region) is that there is an S that is not a P, and what the second diagram does not allow is that there is an S that is a P. On the contrary, the presence of “x” in the diagrams of the two particular sentences (I and O) indicates that the I-sentence is committed to the existence of both an S and a P, and the O-sentence is committed to the existence of an S while remaining noncommittal to the existence of a P.
As we have seen, in traditional logic all four types of categorical sentences are committed to the existence of things that are S and things that are P, while in modern logic only the particular sentences (I and O) have existential import. That difference affects most of the relations in the square of opposition. Since for the contemporary logic the universal sentences are not committed to the existence of things that fall under their terms while particular sentences are, the later are not logical consequences of the former. A-sentences do not entail the I-sentences with the same subject and predicate, and E-sentences do not entail the corresponding O sentences. So, the relation of subalternation on the left and the right side of the square is no longer a valid immediate inference. In addition, we can no longer draw conclusions based on the relation between contraries on the top side of the square. For traditional logic, the truth of one of the universal sentences (A or E) implies the falsehood of the other. Тhis is no longer the case as both sentences are true when there are no S. The sentences “If something is an S, then it is a P” and “If something is an S, then it is not a P” are compatible when the extension of S is empty. Thus, from the truth or the falsehood of a universal sentence no conclusion can be drawn about the truth or falsehood of the other universal sentence, which makes the relation between contraries rather useless form logical point of view. The situation is the same for the relation between subcontraries on the bottom side of the square. The only logical relation that remains intact is between the contradictories on the diagonals – A-sentences continue to be the exact negations of the O-sentences with the same subject and predicate, and similarly for E and I-sentences. This is so because if we deny that the region of those S that are not P is empty (this is how the negation of an A-sentence is interpreted through a Venn diagram), what we are saying is that the region has at least one element, i.e. that at least one S is not P. It is equally apparent that I-sentences are the exact negations of E-sentences with the same subject and predicate.
The change in the understanding of categorical sentences affects also the immediate inference of conversion. Conversion (by limitation) of A-sentences is no longer a valid inference for the same reason that subalternation is no longer such an inference. Since an A-sentence (“All S are P”, SaP) is not committed to the existence of an S or a P and it is true when there are no such entities, it cannot imply a sentence that commits itself to the existence of both (“There is at least one P that is S”, PiS) and will be false if there are no such things. Thus, according to the modern view, the immediate inference of conversion should be modified as follows: E and I-sentences are converted to E and I-sentences, respectively; and A and O-sentences cannot be validly converted.
The change in the understanding of categorical sentences leads to a change in the syllogistic theory – from 24 the valid syllogisms become 15. Let us see why.
Taken in isolation, a sentence involves two terms (the subject and the predicate), which is why in the diagrams above for each sentence there were two circles and four regions (a region for the things that are both S and P, that are S but not P, … etc.). A syllogism involves three terms, which is why in a Venn diagram for it there are three circles and eight regions. The diagram for a syllogism looks like this:
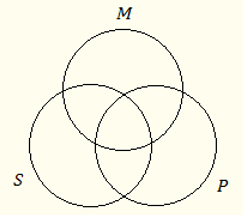
The circles of S, M and P are arranged in such a way that there is a region for each of the possible combinations for an entity falling under no, some, or every of the terms – a total of eight combinations. The innermost segment corresponds to the things that are at the same time S, P, and M. It is bordered by three segments that correspond to things that are S and M but not P, M and P but not S, and S and P but not M. Bordering on the latter, and beyond, are three segments corresponding to things falling under one term but not under the other two. Finally, the region outside the three circles corresponds to the things that are neither S nor M nor P.
Let us verify through a Venn diagram the validity of the most famous syllogism, AAA-1 (Barbara)
| MaP |
| SaM |
| SaP |
An inference is logically valid when the information contained in the conclusion is part of the information contained in the premises (that is when the premises imply the conclusion). Venn diagrams make it possible to check if this is true. For our syllogism, we do this as follows. Taking account of the major premise (“All M are P”), we focus on the relation between M and P abstracting from the circle of S. As we have seen, “All M are P” (MaP) is represented through a Venn diagram by marking as empty the region of those M that are not P:
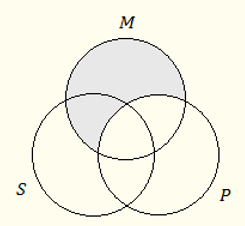
Next, we add the information contained in the second premise “All S are M” (SaM). This is done by marking as empty the region of those S that are not M:

Thus, the diagram expresses all the information contained in the premises. It remains to see whether this information contains the information expressed by the conclusion “All S are P”. The latter will be true if the region of those S that are not P is empty. The diagram shows that this is the case; so, the syllogism is valid.
As a further example, let us check the validity of EIO-1 (Ferio):
| MeP |
| SiM |
| SoP |
The first premise “No M are P” (MeP) is represented by shading the region of those M that are P:

The second premise “Some S are M” (SaM) is represented by placing “x” in the region of those S that are M. Part of this segment has already been declared empty by the other premise, but the other part (the one corresponding to those S that are M but not P) is not such, so we put an “x” in it:

This shows why in a Venn diagram we have to represent the universal premises first. They declare certain regions empty. If we first account for the particular premises, we may put the “x” into a region that the universal premise will then declare empty. There is no such possibility in the reverse order – once the universal premises have determined which regions are empty, we will put the “x” where possible (if not, then the premises contradict each other, and everything follows from them).
The diagram shows that the region of those S that are not P is not empty. Therefore, the conclusion “Some S are not P” follows from the premises, i.e. the syllogism is logically valid.
Let us now see why certain syllogisms that are valid for traditional logic cease to be so from the contemporary perspective. Such is, for example, the AAI mood of the third figure (AAI-3):
| MaP |
| MaS |
| SiP |

The above diagram is obtained after marking as empty the regions of those M that are not P and of those M that are not S. Thus, we have accounted for the information contained in the premises. For the syllogism to be valid, the region of those S that are not P should not be empty, i.e. there has be “x” in it. However, the “x” is nowhere to come from, as it comes from particular premises. Therefore, this and any other syllogism with universal premises and a particular conclusion are invalid.
The valid syllogisms for traditional logic that are not valid for modern logic are precisely those that have two universal premises and a particular conclusion. The table below lists all valid syllogisms for traditional logic. Those of them that are not valid for modern logic are enclosed in parentheses.
| I figure | II figure | III figure | IV figure |
| AAA-1 | EAE-2 | (AAI-3) | (AAI-4) |
| ЕАЕ-1 | AEE-2 | IAI-3 | AEE-4 |
| AII-1 | EIO-2 | AII-3 | (EAO-4) |
| EIO-1 | AOO-2 | (EAO-3) | IAI-4 |
| (AAI-1) | (EAO-2) | EIO-3 | EIO-4 |
| (EAO-1) | (AEO-2) | OAO-3 | (AEO-4) |
As we can see, invalid from contemporary point of view are those and only those syllogisms that have two universal premises and a particular conclusion. It turns out that while for traditional logic the valid syllogisms are 24 (six in each figure), for modern logic they are 15 (four in the first, the second and the third figure and three in the fourth). All syllogisms that are valid for traditional logic and invalid for modern logic can also become valid for the latter if we add as additional premises that the extensions of the terms are not empty (“There are some S”, “There are some M”, “There are some P”). Actually, a closer analysis shows that (with one exception) it will suffice to add as an additional premise only that the extension of the subject of the minor premise (S in the first and the second figure and M in the third and the fourth figure) is not empty. The exception is AEO-4. For it to become valid, we have to assume that the extension of the predicate of the minor premise (S) is not empty.
We can use Venn diagrams to verify the validity of inferences that consist of categorical sentences as the syllogisms but have four rather than three terms. However, to obtain the required 16 regions, a careful drawing is required since we need a diagram similar to one below.
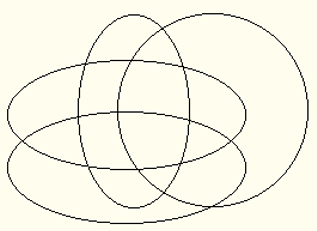
If the terms become five, it is no longer possible to draw in the plane the diagram we need – of five overlapping oval figures containing the required 32 regions.
Exercises
(Download the exercises as a PDF file.)| (1) Prove with Venn diagrams that the following syllogisms are valid: |
| 1) | EАЕ-1 |
| 2) | AII-1 |
| 3) | EIO-2 |
| 4) | AOO-2 |
| 5) | IAI-3 |
| 6) | EIO-3 |
| 7) | OAO-3 |
| 8) | AEE-4 |
| 9) | IAI-4 |

