2.6 Диаграми на Вен
Диаграмите на Вен са измислени в края на 19-ти век (Venn, 1880) и, така да се каже, се намират някъде в междинната територия между традиционната и съвременната логика, защото от една страна служат за определяне на логическата валидност на изводи, съставени изключително от категорични твърдения (най-вече силогизми), но от друга страна самите категорични твърдения се анализират така както го прави съвременната, а не традиционната логика.
Няколко пъти вече беше споменато, че в традиционната логика мълчаливо се предпоставя, че термините в категоричните твърдения не са празни. В това може да се убедим от начина, по който се третират отношенията в логическия квадрат и по специално отношението на подчиненост. Последното се състои в това, че от всяко общо-утвърдително изречение следва частно-утвърдително със същия субект и предикат, и от всяко общо-отрицателно – частно-отрицателно. Частно-утвърдителното изречение обаче може да се перифразира с „Съществува поне едно S, което е P“, в което очевидно се съдържа, че съществува поне едно S и поне едно P. Съответно всяко частно-отрицателно твърдение се перифразира с изречението „Съществува поне едно S, което не е P“, в което се съдържа, че съществува поне едно S, без да има информация дали съществуват P-та. Тъй като частно-утвърдителното следва от общо-утвърдителното, а частно-отрицателното – от общо-отрицателното, излиза, че в общо-утвърдителното скрито се твърди, че съществуват S-ове и P-та, a в общо отрицателното – че съществуват S-ове; ако не беше така, истинността на общите твърдения не би могла да гарантира истинност на частните, защото тогава за А-твърдението щеше да е възможно да е истинно, когато не съществуват S-ове или P-та, а за Е-твърдението – когато не съществуват S-ве, но тогава I и О-твърденията са задължително неистинни. Така че в традиционната логика се предпоставя, че както субектите, така и предикатите на двете утвърдителни и субектите на двете отрицателни твърдения не са празни. Но заради операцията обръщане е необходимо и предикатът на общо-отрицателното да не е празен, защото от всяко общо-отрицателно твърдение следва общо-отрицателно, в което предикатът на първото е станал субект, а субектът на общо-отрицателното не е празен. Няма как такова следване да е налице, ако е възможно предикатът на общо-отрицателното да е празен. Остана да видим, че в традиционната логика се предпоставя и че предикатът на частно-отрицателното твърдение не е празен. Това се вижда от следното. Когато твърдим едно частно-отрицателно твърдение, общо-отрицателното (Е) твърдение със същия субект и предикат разбира се съществува и е истинно или неистинно. Ако е истинно, предикатът му не е празен (вече видяхме това) и следователно не е празен и предикатът на частно-отрицателното, който е същият. Ако Е-твърдението е неистинно, тогава (по логическия квадрат) I-твърдението е истинно, поради което предикатът му не е празен, и значи не е празен и предикатът на частно-отрицателното (O) твърдение, който е същият. Видяхме защо в традиционната логика се предпоставя, че както субектът, така и предикатът на което и да е категорично твърдение не е празен.
Напротив, в съвременната логика (и при диаграмите на Вен) единствено от частните твърдения следва нещо за съществуването на неща, които попадат под термините им. По-конкретно от I-твърдението следва, че съществуват S-ове и P-та, а от O-твърдението – че съществуват S-ове, без да има информация дали съществуват P-та. В общо-утвърдителното и общо-отрицателното не се съдържа никаква информация за съществуването на S-ове или P-та. Това е така, защото общо-утвърдителното „Всяко S е P“ се разглежда като синонимно на изречението „Ако едно нещо е S, то е P“, а общо-отрицателното „Нито едно S не е P“ – като синонимно на „Ако едно нещо е S, то не е P“. Вторите твърдения са тривиално истинни, когато не съществуват S-ове, без значение дали съществуват P-та, или не. Резултатът е, че А и Е-твърденията могат да са истинни и са истинни, когато не съществуват нито S-ове, нито P-та.
Тази разлика между съвременната и традиционната логика в третирането на категоричните твърдения води до значителни разлики между тях при логическия квадрат, операцията обръщане и валидността на силогизмите, които ще разгледаме по-долу.
Сега да видим какво представляват диаграмите на Вен. Следните диаграми отговарят на четирите категорични твърдения:

Всеки от термините (субектът S и предикатът P) има свой кръг, като положението на кръговете един спрямо друг е фиксирано по показания начин. Вътрешността на всеки кръг отговаря на множеството от нещата, които попадат под съответния термин, а пространството извън кръга – на множеството от нещата, които не попадат под термина. По този начин се получават четири сегмента, отговарящи на четири множества – някои от тях евентуално празни. Приличащото на леща сечение на двата кръга отговаря на нещата, които са едновременно S и P; пространството извън двата кръга – на нещата, които не са нито S, нито P; сегментът на S, приличащ на изядена отдясно луна – на нещата, които са S, но не са P; сегментът на P, приличащ на изядена отляво луна – на нещата, които са P, но не са S. Всеки от сегментите може да бъде маркиран по два възможни начина – или като се защрихова (при нас това става със сив цвят), или като в него да се постави „x“. Защриховането на един сегмент означава, че той е празен; слагането на „x“ в него – че не е празен; липсата на „x“ и защриховане – че липсва информация за това, дали е празен, или не .
В горната лява диаграма като празен е маркиран сегментът на нещата, които са S, но не са P. По този начин диаграмата изразява положението на нещата, че няма S-ове, които не са P-та, с други думи, че ако нещо е S, то е P („Всяко S e P“).
В горната дясна диаграма като празен е маркиран сегментът на нещата, които са едновременно S и P. По този начин диаграмата ни казва, че няма S-ове, които да са P, т.е. ако нещо е S, то не е P („Нито едно S не е P“).
В долната лява диаграма има „x“ в сегмента на тези S-ове, които са P. Тъй като „x“ означава съществуване, диаграмата ни казва, че има поне едно S, което е P („Някои S са P“).
Диаграмата долу вдясно съдържа информацията, че множеството на S-овете, които не са P, не е празно, т.е. – че има поне едно S, което не е P („Някои S не са P“).
В диаграмите на общо-утвърдителното и общо-отрицателното твърдение (горните две) не се съдържа информация относно съществуването на каквото и да е. Единственият начин да се изрази съществуване в диаграма на Вен е като се постави „x“ в някой от сегментите; липсата на „x“ (заедно с липсата на защриховане) не означава, че сегментът е празен, а че липсва информация. Като резултат и двете диаграми допускат всеки от четирите възможни случая за S и P – и двата термина да са празни (да няма нито S-ве, нито P-та); и двата да не са празни (да съществуват S-ове и P-та); единият да е празен, а другия – не (да съществуват S-ове, но не и P-та, и обратно). Това което първата диаграма не допуска (посредством защриховането на съответния сегмент) е да съществуват S-ове, които не са P-та, а това което не допуска втората диаграма, е да съществуват S-ове, които са P-та. Напротив, наличието на „x“ в диаграмите на двете частни твърдения показва, че частно-утвърдителното се ангажира със съществуването както на S-ове, така и на P-та, а частно-отрицателно – със съществуването S-ве, като остава неутрално по отношението на съществуването на P-та.
Както видяхме, за традиционната логика всяко от четирите категорични твърдения се ангажира със съществуването на неща, които са S, и неща, които са P, докато за съвременната логика само при частните твърдение (I и O) има някакво ангажиране със съществуване. Тази разлика има като следствие, че за съвременната логика повечето отношения в логическия квадрат престават да са валидни. Тъй като за съвременната логика общите твърдения не се ангажират с каквото и да е съществуване, няма как от тях да следват съответните частни твърдения, тъй като последните се ангажират със съществуването на определени неща. По този начин отношението на подчиненост в логическия квадрат спира да е валидно. Същото важи за отношението на противност. В традиционната логика се приема, че от истинността на едното от общите твърдения следва неистинността на другото, но за съвременната логика това не е така, защото и двете могат да са истинни, ако терминът на субекта е празен. Както изречението „Ако нещо е S, то е P“, така и изречението „Ако нещо е S, то не е P“ допуска възможността S-ове да не съществуват. Резултатът е, че от истинността или неистинността на общо-утвърдителното или общо-отрицателното твърдение не може да се каже нищо за истинността или неистинността на другото общо. Същото е положението и при отношението на подпротивност на долната страна на квадрата. Единственото отношение в логическия квадрат, което се запазва, е това по диагоналите – А-твърдението продължава да е точно отрицание на O-твърдението и E-твърдението – на I-твърдението. Това е така, защото, ако отречем, че сегментът на тези S, които не са P, е празен (това е начинът, по който отрицанието на А-твърдението се интерпретира с диаграма на Вен), това което всъщност казваме е, че въпросният сегмент има поне един елемент, т.е. че поне едно S не е P. По същия начин се вижда и че I-твърдението е отрицание на Е-твърдението.
Промяната в третирането на категоричните твърдение се отразява и върху непосредствения извод на обръщането. Операцията спира да е валидна за А-твърденията по същата причина, поради която спира да е валидно отношението на подчиненост – А-твърдението не се ангажира със съществуването на S-ове или P-та, затова от него няма как да следва твърдение, което се ангажира със съществуването и двете („Съществува поне едно P, което е S“). Така операцията обръщане се променя по следния начин: Е и I-твърденията се обръщат съответно в Е и I-твърдения, а А и О-твърденията не могат да се обръщат .
Промяната в разбирането за категоричните твърдения води и до промяна в броя на валидните силогизми – от 24 те стават 15. Нека видим защо е така.
В едно единствено твърдение участват 2 термина, поради което в горните диаграми сегментите бяха 4 – по един за нещата, които са едновременно S и P, които са S, но не са P, … и т.н. В един силогизъм обаче участват 3 термина, поради което сегментите в диаграмите на Вен за силогизми и изобщо за изводи, в които участват 3 термина, са два пъти повече – 8. Тогава диаграмите на Вен приемат следния общ вид:

Кръговете на S, M и P са разположени по такъв начин, че да има сегмент за всеки от възможните комбинации за попадане на нещо под някой от термините, общо 8 на брой. Най-вътрешният сегмент отговаря на нещата, които са едновременно S, P и M. С него граничат три сегмента, които отговарят съответно на нещата, които са S и M, но не и P, М и P, но не и S, и S и P, но не и М. Граничещи с последните, и по-навън, са три сегмента, които отговарят на нещата, попадащи под единия термин, но не и под другите два. И накрая, пространството извън трите кръга отговаря на нещата, които не са нито S, нито M и нито P.
Ще използваме диаграма на Вен, за да проверим валидността на най-известния от силогизмите – Barbara (AAA-1):
| MaP |
| SaM |
| SaP |
Един извод е валиден, когато информацията, съдържаща се в заключението, е част от информацията, съдържаща се в предпоставките. Диаграмите на Вен дават възможност нагледно да се провери дали е така. В случая това става по следния начин. Първо, абстрахирайки се от кръга на S, представяме отношението между M и P, което отговаря на голямата предпоставка „MaP“ („Всяко M е P“). Както видяхме, това става като маркираме като празен сегментът на тези М, които не са P:

След това, добавяме информацията, съдържаща се във втората предпоставка „SaM“ („Всяко S е М“). Това става като маркираме като празен сегментът на тези S, които не са M:

Така в диаграмата е налице цялата информация, съдържаща се в предпоставките. Остава да видим дали в тази информация се съдържа това, което ни казва заключението „SaP“. Заключението би следвало от предпоставките, ако сегментът на тези S, които не са P, е празен. Диаграмата показва, че това е така, и че (както очаквахме) силогизмът е валиден.
Като следващ пример нека проверим валидността на Ferio (EIO-1):
| MeP |
| SiM |
| SoP |
Първата предпоставка „MeP“ („Нито едно М не е P“) се представя чрез защриховане на сегмента на тези M, които са P:

Втората предпоставка „SiM“ („Някои S са М“) се представя чрез поставяне на „x“ в сегментът на тези S, които са M. Част от този сегмент вече е обявена за празна от другата предпоставка, но другата част от него (тази, отговаряща на S-овете, които са М, но не са P) не е такава, така че слагаме „x“ в нея:

Това показва защо в диаграмите на Вен трябва да представяме първо общите предпоставки на един извод. Те обявяват определени сегменти за празни и ако представим първо частните предпоставки, има опасност изразяващото съществуване „x“ да се окаже в сегмент, който общите предпоставки да обявят за празен. При обратния ред няма такава опасност – след като общите предпоставки са определили кои сегменти са празни, ще сложим „x“-вете там, където това е възможно (ако не е възможно, значи предпоставките си противоречат).
От диаграмата се вижда, че сегментът на тези S, които не са P, не е празен. Следователно заключението „Някои S не са P“ се съдържа в предпоставките, т.е. силогизмът е валиден.
Нека видим сега защо определени, валидни за традиционната логика силогизми спират да бъдат такива. Такъв е например модус ААI от трета фигура (ААI-3):
| MaP |
| MaS |
| SiP |

Горната диаграма се получава след като маркираме като празни сегментите на тези M, които не са P, и на тези М, които не са S. По този начин информацията, съдържаща се в предпоставките, е въведена в диаграмата. За да е валиден силогизмът, в диаграмата трябва да се съдържа, че сегментът на тези S, които не са P, не е празен, т.е. в него трябва да има „x“. „x“ обаче няма и няма откъде да има, защото и двете предпоставки са общи, а „х“-овете идват от частните предпоставки. Следователно този силогизъм и всеки друг силогизъм с общи предпоставки и частно заключение е невалиден.
Валидните за традиционната логика силогизми, които не са валидни за съвременната логика, са точно тези, които имат две общи предпоставки и частно заключение. В таблицата отдолу са дадени всички валидни за традиционната логика силогизми, като тези от тях, които не са валидни за съвременната логика, са заградени в скоби.
| I фигура | II фигура | III фигура | IV фигура |
| AAA-1 | EAE-2 | (AAI-3) | (AAI-4) |
| ЕАЕ-1 | AEE-2 | IAI-3 | AEE-4 |
| AII-1 | EIO-2 | AII-3 | (EAO-4) |
| EIO-1 | AOO-2 | (EAO-3) | IAI-4 |
| (AAI-1) | (EAO-2) | EIO-3 | EIO-4 |
| (EAO-1) | (AEO-2) | OAO-3 | (AEO-4) |
Както се вижда, не са валидни тези и само тези силогизми, които имат две общи предпоставки и частно заключение. По този начин се получава, че докато за традиционната логика валидните силогизми са 24 – по шест във всяка от фигурите, то за съвременната логика валидните силогизми са 15 – по четири в първа, втора и трета фигура и три в четвърта. Всеки от валидните за традиционната логика, но невалидни за съвременната логика силогизми, би станал валиден и за последната, ако като допълнителна предпоставка се приеме принципът, че термините не са празни. Впрочем по-внимателният анализ показва, че всеки от въпросните силогизми с изключение на АЕО-4 би станал валиден, ако като допълнителна предпоставка се приеме само, че субектът на малката предпоставка (малкият термин в първа и втора фигура и средният в трета и четвърта) не е празен. За валидността на АЕО-4 е нужно да се приеме, че не е празен предикатът на малката предпоставка „MeS“.
Диаграмите на Вен могат да бъдат използвани и за проверка на валидността на съставени от категорични твърдения изводи, общият брой на термините в които е не три като при силогизмите, а четири. За да се получат обаче нужните 16 сегмента, е нужно внимателно чертане, подобно на това в долната диаграма.
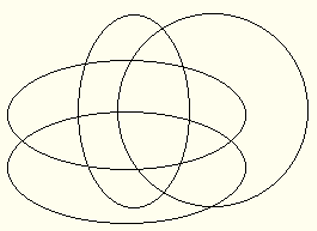
Ако термините станат пет, вече не е възможно в равнината да се начертае диаграма от припокриващи се прости овални фигури, съдържаща нужните ни 32 сегмента.
Задачи
(Изтеглете задачите като pdf.)| (1) Докажете с диаграми на Вен, че следните силогизми са валидни: |
| 1) | EАЕ-1 |
| 2) | AII-1 |
| 3) | EIO-2 |
| 4) | AOO-2 |
| 5) | IAI-3 |
| 6) | EIO-3 |
| 7) | OAO-3 |
| 8) | AEE-4 |
| 9) | IAI-4 |

