Решения
1.1 Конюнкция, дизюнкция отрицание
Задача (1)
1) p – Тази кола е мощна, q – Тази кола е много икономична: ¬p ∧ q
2) p – Павел е виновен, q – Иван е виновен: ¬(p∧¬q)
3) p – Волдемор е подъл, q – Волдемор е жесток: p ∧ q
1.2 Импликация и еквивалентност
Задача (1)
1) p – Следващата година ще сме живи, q – Следващата година ще сме здрави, r – Следващата година ще се видим: (p∧q) → r
2) p – Ще вали дъжд, q – Ще е студено, r – Партито ще е на двора: (p∨q) → ¬r
3) p – Световната рецесия ще продължи, q – Ще се намалят данъците, r – Ще има стагнация, s – Ще има банкови фалити: p → [¬q→(r∧s)]
4) p – Иван е запознат с клаузите на договора, q – Иван ще подпише договора, r – Иван ще изпълнява договора в бъдеще, s – Иван ще плати глоба, t – Имотът на Иван ще бъде конфискуван, u – Иван ще влезе в затвора: (p∧q) → {¬r→[(s∧t)∨u]}
5) p – Иван ще отиде на партито, q – Мария ще отиде на партито: p → ¬q
6) p – Иван ще спре да ти се сърди, q – Ще си вземеш думите назад, r – Ще се извиниш на Иван: p ↔ (q∧r)
1.3 Таблици за истинност
Задача (1)
1) Правилно образуван е.
2) Не е правилно образуван (скобите са излишни).
3) Не е правилно образуван (квадратните скоби са излишни и има нужда от скоби на друго място).
4) Правилно образуван е.
Задача (2)
1) p, q, r, ¬p, ¬q, ¬p∧r, p↔¬q, (¬p∧r)∨(p↔¬q)
Задача (3)
1) конюнкция
2) импликация
3) конюнкция
Задача (4)
1) тавтология
| p | q | q→p | p→(q→p) |
| И | И | И | И |
| И | Н | И | И |
| Н | И | Н | И |
| Н | Н | И | И |
2) синтетична
| p | q | p∨q | ¬(p∨q) | p∧q | ¬(p∨q)→(p∧q) |
| И | И | И | Н | И | И |
| И | Н | И | Н | Н | И |
| Н | И | И | Н | Н | И |
| Н | Н | Н | И | Н | Н |
3) синтетична
| p | q | ¬q | p→¬q | ¬p | (p→¬q)→¬p |
| И | И | Н | Н | Н | И |
| И | Н | И | И | Н | Н |
| Н | И | Н | И | И | И |
| Н | Н | И | И | И | И |
4) тавтология
| p | q | r | ¬q | ¬q∨r | p→(¬q∨r) | ¬p | ¬p∨q | [p→(¬q∨r)]∨(¬p∨q) |
| И | И | И | Н | И | И | Н | И | И |
| И | И | Н | Н | Н | Н | Н | И | И |
| И | Н | И | И | И | И | Н | Н | И |
| И | Н | Н | И | И | И | Н | Н | И |
| Н | И | И | Н | И | И | И | И | И |
| Н | И | Н | Н | Н | И | И | И | И |
| Н | Н | И | И | И | И | И | И | И |
| Н | Н | Н | И | И | И | И | И | И |
1.4 Доказателство чрез допускане на противното
Задача (1)
2)
| 1. | (p→q)→[(r∨p)→(r∨q)] – Н допускане |
| 2. | p→q – И от 1. |
| 3. | (r∨p)→(r∨q) – Н от 1. |
| 4. | r∨p – И от 3. |
| 5. | r∨q – Н от 3. |
| 6. | r – Н от 5. |
| 7. | q – Н от 5. |
| 8. | p – И от 4. и 6. |
| 9. | p→q – Н от 8. и 7. – противоречие с 2. |
3)
| 1. [p∨(q∧¬r)]→[(p∨q)∧(r→p)] – Н допускане | |
| 2. p∨(q∧¬r) – И от 1. | |
| 3. (p∨q)∧(r→p) – Н от 1. | |
| 4. p – И от 2. (1-ви случай) | 4. q∧¬r – И от 2. (2-ри случай) |
| 5. p∨q – И от 4. | 5. q – И от 4. |
| 6. r→p – Н от 3. и 5. | 6. ¬r – И от 4. |
| 7. p – Н от 6. – противоречие с 4. | 7. r – Н от 6. |
| 8. p∨q – И от 5. | |
| 9. r→p – Н от 3. и 8. | |
| 10. r – И от 9. – противоречие с 7. | |
Задача (2)
1)
| 1. | (¬q→¬p)∧¬(q∨¬p) – И допускане |
| 2. | ¬q→¬p – И от 1. |
| 3. | ¬(q∨¬p) – И от 1. |
| 4. | q∨¬p – Н от 3. |
| 5. | q – Н от 4. |
| 6. | ¬p – Н от 4. |
| 7. | ¬q – И от 5. |
| 8. | ¬q→¬p – Н от 7. и 6. – противоречие с 2. |
1.5 Истинностно-функционален анализ
Задача (1)
1) тавтология
| p→(q→p) | |
| p: И | p: Н |
| И→(q→И) | Н→(q→Н) |
| И→И | И |
| И | |
3) тавтология
| (¬p∨¬q)→¬(p∧q) | |
| p: И | p: Н |
| (Н∨¬q)→¬(И∧q) | (И∨¬q)→¬(Н∧q) |
| ¬q→¬q | И→¬Н |
| И | И→И |
| И | |
4) синтетична
| [(p→q)→r]↔[p→(q→r)] | |
| p: И | p: Н |
| [(И→q)→r]↔[И→(q→r)] | [(Н→q)→r]↔[Н→(q→r)] |
| [q→r]↔[q→r] | [И→r]↔И |
| И | И→r |
| r | |
| r: Н | |
| Н | |
Задача (2)
2)
| (p→q)→[(r∨p)→(r∨q)] | |
| r: И | r: Н |
| (p→q)→[(И∨p)→(И∨q)] | (p→q)→[(Н∨p)→(Н∨q)] |
| (p→q)→[И→И] | (p→q)→[p→q] |
| (p→q)→И | И |
| И | |
1.6 Логическо следване и логическа еквивалентност
Задача (1)
6) За да проверим дали схемата е валидна, свързваме конюнкцията на предпоставките в импликация с заключението и получаваме формулата „[(p∨¬q)∧(¬q↔¬p)]→(p→¬q)“. Схемата ще е валидна, ако тази формула е тавтология. Проверяваме дали е тавтология с таблица за истинност или с истинностно функционален анализ:
| [(p∨¬q)∧(¬q↔¬p)]→(p→¬q) | |
| p: И | |
| [(И∨¬q)∧(¬q↔Н)]→(И→¬q) | |
| [И∧¬¬q]→¬q | |
| ¬¬q→¬q | |
| q: И | |
| И→Н | |
| Н | |
Формулата не е тавтология, следователно схемата за извод не е валидна.
Задача (2)
2) Представяме символно простите изречения например така: „p“ – „Компанията е виновна“, „q“ – „Софтуерът е на компанията“, „r“ – „Софтуерът е бил инсталиран преди януари“. Тогава а) се представя символно с „p↔(q∧r)“, а b) – с „[q→(r∧p)]∧[¬q→(¬r∧¬p)]“. За да проверим дали от първото следва второто, ги свързваме в импликация и проверяваме (с таблица за истинност или с истинностно-функционален анализ) дали получената формула е тавтология:
| [p↔(q∧r)]→{[q→(r∧p)]∧[¬q→(¬r∧¬p)]} | |
| q: И | |
| [p↔(И∧r)]→{[И→(r∧p)]∧[Н→(¬r∧¬p)]} | |
| [p↔r]→{(r∧p)∧И} | |
| (p↔r)→(r∧p) | |
| p: Н | |
| (Н↔r)→(r∧Н) | |
| ¬r→Н | |
| ¬¬r | |
| r | |
Формулата не е тавтология, следователно от a) не следва b).
Задача (3)
4) За да докажем, че формулите са логически еквивалентни, ги свързваме с (материална) еквивалентност и показваме (с таблица за истинност или с истинностно-функционален анализ), че получената формула е тавтология:
| (р↔q)↔[(p∧q)∨(¬p∧¬q)] | |
| p: И | p: Н |
| (И↔q)↔[(И∧q)∨(Н∧¬q)] | (Н↔q)↔[(Н∧q)∨(И∧¬q)] |
| q↔[q∨Н] | ¬q↔[Н∨¬q] |
| q↔q | ¬q↔¬q |
| И | И |
10) По същия начин:
| [р∧(q∨r)]↔[(р∧q)∨(р∧r)] | |
| p: И | p: Н |
| [И∧(q∨r)]↔[(И∧q)∨(И∧r)] | [Н∧(q∨r)]↔[(Н∧q)∨(Н∧r)] |
| (q∨r)↔(q∨r) | Н↔(Н∨Н) |
| И | Н↔Н |
| И | |
Задача (4)
4) Представяме простите твърдения (например) така: „p“ – „Иван е виновен“, „q“ – „Петър е невинен“, r – „Стоян е излъгал“. Тогава a) се представя символно с „p→(q∧r)“, а b) – с „(¬r→¬p)∧(p→q)“. За да проверим дали двете са логически еквивалентни, ги свързваме с еквивалентност и проверяваме (с таблица за истинност или с истинностно-функционален анализ) дали получената формула е тавтология:
| [p→(q∧r)]↔[(¬r→¬p)∧(p→q)] | |
| p: И | p: Н |
| [И→(q∧r)]↔[(¬r→Н)∧(И→q)] | [Н→(q∧r)]↔[(¬r→И)∧(Н→q)] |
| (q∧r)↔(¬¬r∧q) | И↔(¬r∧И) |
| (q∧r)↔(r∧q) | ¬r |
| И | Н И |
Формулата не е тавтология, следователно a) и b) не са логически еквивалентни.
1.7 Бърза проверка за логическо следване
Задача (1)
3) Предпоставката е истинна само когато „p“, „r“ и „s“ са едновременно истинни. Проверяваме дали тогава е възможно заключението да е неистинно:
| r ↔ (p→s) |
| p: И, r: И, s: И |
| И ↔ (И→И) |
| И↔И |
| И |
Когато предпоставката е истинна, заключението е истинно, следователно схемата за извод е валидна.
8) Заключението е неистинно само когато „p“ и „q“ са И, а „r“ e Н. Проверяваме дали тогава е възможно предпоставката да е истинна:
| (p∧¬q) ∨ [(r∧s)→p] |
| p: И, q: И, r: Н |
| (И∧Н) ∨ [(Н∧s)→И] |
| Н ∨ И |
| И |
Когато заключението е неистинно, предпоставката е истинна, следователно схемата за извод не е валидна.
Задача (2)
2) Представяме символно простите твърдения например така: „p“ – „Нашият представител ще се кандидатира за президент“, „q“ – „Нашият представител ще направи позитивна кампания“, „r“ – „Нашият представител ще стигне до балотаж“, „s“ – „Нашият представител ще спечели изборите“, „t“ – „Нашият представител ще бъде преизбран след 4 години“, „u“ – „Нашият представител ще подкрепи смъртното наказание“. Тогава аргументът се представя символно така:
| p → (q→r) |
| (r∧s) → ¬t |
| u → (s∧t) |
| p → (q→¬u) |
Заключението му е неистинно само когато „p“, „q“ и „u“ са И, затова проверяваме дали в този случай конюнкцията от предпоставките може да е И:
| [p→(q→r)] ∧ [(r∧s)→¬t] ∧ [u→(s∧t)] | ||
| p: И, q: И, u: И | ||
| [И→(И→r)] ∧ [(r∧s)→¬t] ∧ [И→(s∧t)] | ||
| r ∧ [(r∧s)→¬t] ∧ (s∧t) | ||
| r: И | r: Н | |
| И ∧ [(И∧s)→¬t] ∧ (s∧t) | Н ∧ [(Н∧s)→¬t] ∧ (s∧t) | |
| (s→¬t) ∧ (s∧t) | Н | |
| s: И | s: Н | |
| (И→¬t) ∧ (И∧t) | (Н→¬t) ∧ (Н∧t) | |
| ¬t ∧ t | И ∧ Н | |
| Н | Н | |
Когато заключението е неистинно, конюнкцията от предпоставките също е неистинна, което означава, че при неистинно заключение не е възможно всички предпоставки да са истинни, следователно схемата за извод е валидна.
1.8 Естествена дедукция
Задача (1)
5)
| 1. F→G |
| 2. ¬(F∧G)∧L |
| 3. (G∨H)→(I∧J) |
| 4. F∨(K∨G) |
| 5. ¬K∧L / I∨H |
| 6. F→(F∧G) от 1. по абсорбиране |
| 7. ¬(F∧G) от 2. по симплификация |
| 8. ¬F от 6. и 7. по модус толенс |
| 9. K∨G от 4. и 8. по дизюнктивен силогизъм |
| 10. ¬K от 5. по симплификация |
| 11. G от 9. и 10. по дизюнктивен силогизъм |
| 12. G∨H от 11. по добавяне |
| 13. I∧J от 3. и 12. по модус поненс |
| 14. I от 13. по симплификация |
| 15. I∨H от 14. по добавяне |
Задача (2)
1)
| 1. А∨¬B |
| 2. ¬C→¬A / B→C |
| 3. ¬B∨A от 1. по комутация |
| 4. B→A от 3. по материална импликация |
| 5. A→C от 2. по транспозиция |
| 6. B→C от 4. и 5. по хипотетичен силогизъм |
Задача (3)
5)
| 1. (L∧M)→N |
| 2. (L∧¬M)→¬N / L→(M↔N) |
| 3. L→(M→N) от 1. по експортиране |
| 4. L→(¬M→¬N) от 2. по експортиране |
| 5. L→(N→M) от 4. по транспозиция |
| 6. ¬L∨(M→N) от 3. по материална импликация |
| 7. ¬L∨(N→M) от 5. по материална импликация |
| 8. [¬L∨(M→N)]∧[¬L∨(N→M)] от 6. и 7. по конюнкция |
| 9. ¬L∨[(M→N)∧(N→M)] от 8. по дистрибуция |
| 10. ¬L∨(M↔N) от 9. по материална еквивалентност |
| 11. L→(M↔N) от 10. по материална импликация |
Задача (4)
5)
| 1. (L∧M)→N |
| 2. (L∧¬M)→¬N / L→(M↔N) |
| 3. L→(M→N) от 1. по експортиране |
| 4. L→(¬M→¬N) от 2. по експортиране |
| 5. L→(N→M) от 4. по транспозиция |
| 6. L допускане |
| 7. M→N от 3. и 6. по модус поненс |
| 8. N→M от 5. и 6. по модус поненс |
| 9. (M→N)∧(N→M) от 7. и 8. по конюнкция |
| 10. M↔N от 9. по материална еквивалентност |
| 11. L→(M↔N) от 6. – 10. по условно доказателство |
Задача (5)
3) Простите твърдения в аргумента са следните: „L“ – „Лекарят ще инжектира антителата“, „A“ – „Пациентът ще получи алергична реакция“, „C“ – „Черният дроб на пациента ще спре да функционира“, „V“ – „Вирусът ще се разпространи в кръвоносната система на пациента“, „S“ – „Пациентът ще доживее до сутринта“. Аргументът се представя символно така:
| (L→A)∧(A→C) |
| ¬L→V |
| V→C |
| C→¬S |
| L∨¬L |
| ¬S |
Следват две доказателства за неговата валидност – без и със използване на допускане:
| 1. (L→A)∧(A→C) |
| 2. ¬L→V |
| 3. V→C |
| 4. C→¬S |
| 5. L∨¬L / ¬S |
| 6. L→A от 1. по симплификация |
| 7. (L→A)∧(¬L→V) от 6. и 2. по конюнкция |
| 8. A∨V от 5. и 7. по конструктивна дилема |
| 9. A→C от 1. по комутация и симплификация |
| 10. A→¬S от 9. и 4. по хипотетичен силогизъм |
| 11. V→¬S от 3. и 4. по хипотетичен силогизъм |
| 12. (A→¬S)∧(V→¬S) от 10. и 11. по конюнкция |
| 13. ¬S∨¬S от 8. и 12. по конструктивна дилема |
| 14. ¬S от 13. по тавтология |
| 1. (L→A)∧(A→C) |
| 2. ¬L→V |
| 3. V→C |
| 4. C→¬S |
| 5. L∨¬L / ¬S |
| 6. ¬¬S допускане |
| 7. ¬C от 4. и 6. по модус толенс |
| 8. ¬V от 3. и 7. по модус толенс |
| 9. L от 2. и 8. по модус толенс и двойно отрицание |
| 10. L→A от 1. по симплификация |
| 11. A от 9. и 10. по модус поненс |
| 12. A→C 1. по комутация и симплификация |
| 13. C от 11. и 12. по модус поненс – противоречие с 7. |
| 14. ¬S от 6. – 13. по свеждане до противоречие |
1.9 Логически преобразувания
Задача (1)
1) Изразът е както в нормална дизюнктивна, така и в нормална конюнктивна форма.
10) Изразът не е нито в нормална дизюнктивна, нито в нормална конюнктивна форма.
Задача (2)
11)
| [(r→¬s)→r] ∧ {(r∧s) ∨ [¬r→¬(p→q)]} |
| [¬(r→¬s)∨r] ∧ {(r∧s) ∨ ¬¬r ∨ ¬(p→q)} |
| [(r∧¬¬s)∨r] ∧ {(r∧s) ∨ r ∨ (p∧¬q)} |
| r ∧ {r ∨ (p∧¬q)]} |
| r |
Задача (3)
4) Долните преобразувания показват, че двете формули се свеждат до една и съща формула, следователно са логически еквивалентни:
| p → (¬q∧r) | (p→¬q) ∧ (p→r) | |
| ¬p ∨ (¬q∧r) | (¬p∨¬q) ∧ (¬p∨r) | |
| (¬p∨¬q) ∧ (¬p∨r) |
Задача (5)
3) Долните преобразувания показват, че формулата се свежда до израз с формата „α→α“, следователно е тавтология:
| [p∨(q∧¬r)] → [(p∨q)∧(r→p)] |
| [p∨(q∧¬r)] → [(p∨q)∧(¬r∨p)] |
| [p∨(q∧¬r)] → [(p∨q)∧(p∨¬r)] |
| [p∨(q∧¬r)] → [(p∨(q∧¬r)] |
2. Традиционна логика
2.1 Категорични твърдения
Задача (1)
5) Изречението е в стандартна форма. Субект: „активен противник на вдигането на корпоративния данък“; предикат: „член на търговската камара“; общо-утвърдително; символно представяне: SaP.
17) Преформулирано в стандартна форма, твърдението е „Всеки, който е способен да обича, е познал нещастието“. Субект: „способен да обича“; предикат: „познал нещастието“; вид: общо-утвърдително; символно представяне: SaP.
2.2 Логически квадрат
Задача (1)
2) Когато А-твърдението е неистинно, истинностната стойност на Е и на I-твърдението е неопределена, а на О-твърдението е И.
2.3 Непосредствени изводи
Задача (1)
7) По подчиненост можем да изведем „Някои оптимисти не са хора, които познават живота“; по обръщане – „Нито един човек, който познава живота, не е оптимист“; по превръщане – „Всички оптимисти са хора, които не познават живота“; по контрапозиция – „Някои хора, които не познават живота, са оптимисти“.
2.4 Силогизми
Задача (1)
1) Заключението е „Някои космически тела се движат по елиптични орбити“; субектът му „космическо тяло“ е малкият термин, а предикатът му „нещо, което се движи по елиптична орбита“ е големият термин. Средният термин е „планета“. Голямата предпоставка съдържа големия термин; значи тя е твърдението „Всички планети се движат по елиптични орбити“. Другата предпоставка, „Всички планети са космически тела“, е малката предпоставка. Преформулиран в стандартна форма, силогизмът е следният:
| Всички планети се движат по елиптични орбити. |
| Всички планети са космически тела. |
| Някои космически тела се движат по елиптични орбити. |
Символното му представяне е:
| MaP |
| MaS |
| SiP |
Типът му е AAI-3.
Задача (2)
1)
| 1. PeM |
| 2. SiM / SoP |
| 3. MeP от 1. по обръщане |
| 4. SоP от 3. и 2. по Ferio |
2.5 Правила за валидност на силогизмите
Задача (1)
1) В по-разгърнат вид IAI-2 се представя символно така:
| PiM |
| SaM |
| SiP |
Единственото нарушено правило е, че средният термин не е разпределен в нито една от предпоставките.
Задача (2)
1) Аргументът се представя символно с
| MoP |
| SaM |
| SoP |
където „S“ отговаря на „добър физик“, „M“ – на „добър математик“, а „P“ – на „има добро пространствено въображение“. Силогизмът нарушава правилото, че средният термин трябва да е разпределен поне в една от предпоставките, т.е. аргументът не е валиден.
2.6 Диаграми на Вен
Задача (1)
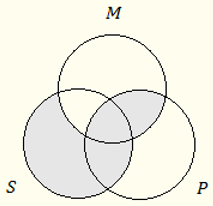
1) Представен символно в по-разгърнат вид EAE-1 e следният силогизъм:
| MeP |
| SaM |
| SeP |
Долната диаграма на Вен показва, че е логически валиден.
3. Предикатна логика
3.1 Общи и единични термини
Задача (1)
2) общ термин
Задача (2)
5) „F“ – „…е похвално“, „a“ – „това, което каза сега“, „b“ – „това, което каза по-рано“: Fa ∧ ¬Fb
3.2 Квантори и променливи
Задача (1)
4) Обхватът на „∃х“ е „Fxy ∧ ∀yGyx“; обхватът на „∀y“ е „Gyx“. Двете участия на „x“ са свързани; първото участие на „y“ е свободно, а второто е свързано. Изразът представя символно отворено изречение.
Задача (2)
14) ∃x(Hx ∧ Gx ∧ Fax)
3.3 Възможностите на езика на предикатната логика
Задача (1)
12) ∀x[(Fx ∧¬Hxa) → Gax]
20) ∀x∃y(Fxy ∧ Fya)
Задача (2)
3) ∀x[Hx → ∃y(Hy ∧ Fxy ∧ Fya)]
3.5 Доказателствена процедура
Задача (1)
6) Като преместим отрицанието в първия израз („¬∃x∀y∀z“) от другата страна на кванторите и ги обърнем, получаваме „∀x∃y∃z¬“. Разликата с втория израз („∀x∃y∀z¬“) е само в последния квантор. Следователно, ако в първия израз сменим последния квантор от „∀z“ на „∃z“, изразите ще станат еквивалентни.
Задача (2)
6) Не е правилна. Първото твърдение „¬∀x(Fxa ↔ Gax)“ не е универсално, а е отрицание (за да е правилна, главния логически оператор трябва да е универсален квантор).
Задача (3)
5) И двете инстанциации не са правилни: екзистенциалната – защото инстанциираната константа „а“ вече се среща (трябва да е нова), универсалната – защото твърдението в 1. не е универсално, а е отрицание.
Задача (4)
3) Символно представен, OAO-3 е следната схема за извод:
| ∃x(Mx ∧ ¬Px) |
| ∀x(Mx → Sx) |
| ∃x(Sx ∧ ¬Px) |
| 1. ∃x(Mx ∧ ¬Px) |
| 2. ∀x(Mx → Sx) / ∃x(Sx ∧ ¬Px) |
| 3. ¬∃x(Sx ∧ ¬Px) допускане |
| 4. ∀x¬(Sx ∧ ¬Px) от 3. по връзка между кванторите |
| 5. Ma ∧ ¬Pa от 1. по EI |
| 6. Ma → Sa от 2. по UI |
| 7. ¬(Sa ∧ ¬Pa) от 4. по UI |
| 8. Ma от 5. по симплификация |
| 9. Sa от 8. и 6. по модус поненс |
| 10. ¬Pa от 5. по симплификация |
| 11. Sa ∧ ¬Pa от 9. и 10. по конюнкция – противоречие с 7. |
| 12. ∃x(Sx ∧ ¬Px) от 3.-11. по свеждане до противоречие |
Задача (5)
5)
| 1. ∃x(Fx∧Gx) ∨ ∃x(Fx∧¬Gx) / ∃xFx |
| 2. ¬∃xFx допускане |
| 3. ∀x¬Fx от 2. по връзка между кванторите |
| 4. ∃x[(Fx∧Gx) ∨ (Fx∧¬Gx)] от 1. (разпределимост на екзист. квантор в дизюнкцията) |
| 5. (Fа∧Gа) ∨ (Fа∧¬Gа) от 4. по EI |
| 6. Fа ∧ (Gа∨¬Gа) от 5. по дистрибуция |
| 7. Fa от 6. по симплификация |
| 8. ¬Fa от 3. по UI – противоречие с 7. |
| 9. ∃xFx от 2.-8. по свеждане до противоречие |
Задача (6)
9)
| 1. ∀x[Fx → (Gx ∧ Hx)] |
| 2. ∃x(Hx ∧ ¬Gx) / ∃x(¬Fx ∧ Hx) |
| 3. ¬∃x(¬Fx ∧ Hx) допускане |
| 4. ∀x¬(¬Fx ∧ Hx) от 3. по връзка между кванторите |
| 5. Hа ∧ ¬Gа от 2. по EI |
| 6. Fa → (Ga ∧ Ha) от 1. по UI |
| 7. ¬(¬Fa ∧ Ha) от 4. по UI |
| 8. Fa ∨ ¬Ha от 7. по Де Морган и двойно отрицание |
| 9. Ha от 5. по симплификация |
| 10. Fa от 8. и 9. по дизюнктивен силогизъм |
| 11. Ga ∧ Ha от 10. и 6. по модус поненс |
| 12. Ga от 11. по симплификация |
| 13. ¬Gа от 5. по симплификация – противоречие с 12. |
| 14. ∃x(¬Fx ∧ Hx) от 3.-13. по свеждане до противоречие |
Задача (7)
2) Допускаме отрицанието на „∃x(∀yFy → Fx)“ и стигаме до противоречие:
| 1. ¬∃x(∀yFy → Fx) допускане |
| 2. ∀x¬(∀yFy → Fx) от 1. по връзка между кванторите |
| 3. ¬(∀yFy → Fа) от 2. по UI |
| 4. ∀yFy ∧ ¬Fа от 3. по мат. импликация |
| 5. ∀yFy от 4. по симплификация |
| 6. ¬Fа от 4. по симплификация |
| 7. Fа от 5. по UI – противоречие с 6. |
| 8. ∃x(∀yFy → Fx) от 1.-7. по свеждане до противоречие |
Задача (9)
5) ирефлексивно (никой не е учител на самия себе си); нито симетрично, нито асиметрично (ако а е учител на b, то b или не му е учител, или му е учител по нещо друго); нито транзитивно, нито интранзитивно (ако а е учител на b, а b е учител на c, то a може както да е учител на c, така и да не му е учител)
3.6 Равенство и определени описания
Задача (2)
8) ¬∃x∃y[Fxy ∧ ∀z(z≠y → ¬Fyz)]
Задача (5)
4) ∃x{Fx ∧ Gdx ∧ ∀y[(Fy ∧ Gdy) → x=y] ∧ Hxk}
3.7 Логически преобразувания в предикатната логика
Задача (1)
7) Преобразуваме първия израз във втория със следната поредица от еквивалентности:
| ∀xFxy ↔ ¬∃zGz |
| (∀xFxy → ¬∃zGz) ∧ (¬∃zGz → ∀xFxy) |
| (∀xFxy → ∀z¬Gz) ∧ (∀z¬Gz → ∀xFxy) |
| ∃x(Fxy → ∀z¬Gz) ∧ ∀x(∀z¬Gz → Fxy) |
| ∃x(Fxy → ∀z¬Gz) ∧ ∀x∃z(¬Gz → Fxy) |
Задача (2)
4)
| ∃xFx → [∃xGx ↔ ∃xHx] |
| ∃xFx → [(∃xGx → ∃xHx) ∧ (∃xHx → ∃xGx)] |
| ∃xFx → [(∃yGy → ∃zHz) ∧ (∃wHw → ∃uGu)] |
| ∀x{Fx → [(∃yGy → ∃zHz) ∧ (∃wHw → ∃uGu)]} |
| ∀x{Fx → [∀y(Gy → ∃zHz) ∧ ∀w(Hw → ∃uGu)]} |
| ∀x{Fx → [∀y∃z(Gy → Hz) ∧ ∀w∃u(Hw → Gu)]} |
| ∀x{Fx → ∀y∃z[(Gy → Hz) ∧ ∀w∃u(Hw → Gu)]} |
| ∀x{Fx → ∀y∃z∀w∃u[(Gy → Hz) ∧ (Hw → Gu)]} |
| ∀x∀y∃z∀w∃u{Fx → [(Gy → Hz) ∧ (Hw → Gu)]} |
4. Некласически логики
4.1 Модални логики
Задача (1)
11) ◊f p → □p◊f p
Задача (2)
6) Ако „¬◊□□α“ (първият израз) се промени на „¬◊□◊α“, ще стане еквивалентен на „□◊□¬α“.
Задача (3)
10)

Задача (4)
7)

Задача (5)
7)

Задача (6)
1)
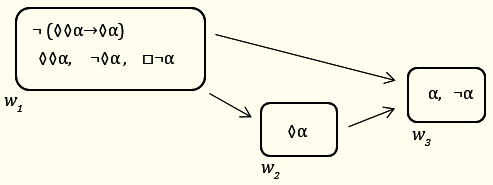
Задача (8)
3)
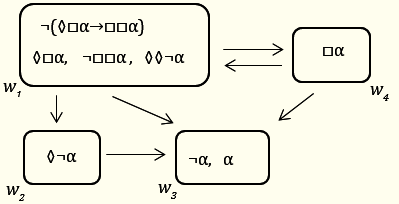
4.2 Тризначни логики
Задача (1)
3) Където стойностите са две, първата е за логиката на Клини, а втората за логиката на Бочвар.
| p | q | ¬p | ¬q | q∧¬q | ¬p∨(q∧¬q) |
| И | И | Н | Н | Н | Н |
| И | # | Н | # | # | # |
| И | Н | Н | И | Н | Н |
| # | И | # | Н | Н | # |
| # | # | # | # | # | # |
| # | Н | # | И | Н | # |
| Н | И | И | Н | Н | И |
| Н | # | И | # | # | И # |
| Н | Н | И | И | Н | И |

