2.2 Логически квадрат
Това, дали едно категорично твърдение е истинно, или не, зависи от отношението между обемите на субекта и на предиката му. Лесно се вижда, че твърдение с формата „Всяко S е Р“ (SaP) е истинно, ако и само ако обемът на S (множеството от нещата, които са S) е подмножество на обемa на Р (множеството от нещата, които са P). При това понятието за подмножество позволява двата обема да съвпадат. Например „Всички хора са разумни“ е истинно, ако и само ако множеството на хората е подмножество на множеството на разумните същества, като в зависимост от това, дали има, или не, други разумни същества освен хората, двете множества може и да съвпадат.
Да разгледаме някои елементарни отношения между две множества, а следователно и между обемите на два термина:
X и Y са различни множества само ако имат различни елементи – ако имат едни и същи елементи, те са едно и също множество. Казваме, че едно множество X е подмножество на едно множество Y (символно, X ⊆ Y), ако и само ако всички елементи на X са елементи на Y. От тази дефиниция следва, че X ще бъде подмножество на Y също и ако елементите на X и Y са едни и същи и следователно са едно и също множество – всяко множество е подмножество на самото себе си (символно, X ⊆ X). Ако X е подмножество на Y и Y e подмножество на X, елементите им ще бъдат едни и съща и те ще бъдат едно и също множество. Ако X е подмножество на Y, но Y не е подмножество на X, с други думи ако всички елементи на X са елементи на Y, но Y има елементи, които не са елементи на X, казваме, че X е строго подмножество на Y (символно, X ⊂ Y).
Две множества са изключващи се, ако и само ако нямат общи елементи. Например, множеството на котките и множеството на папагалите са изключващи се, защото няма нещо, което да е едновременно котка и папагал. От друга страна, множествата на оперните певици и на шофьорите не са изключващи се, защото има поне една оперна певица, която е и шофьор.
Две множества са пресичащи се, ако и само ако имат поне един общ елемент. От това следва, че X и Y са пресичащи се точно когато не са изключващи се.
Следната диаграма показва възможните отношения между обемите на два произволни термина S и P:1
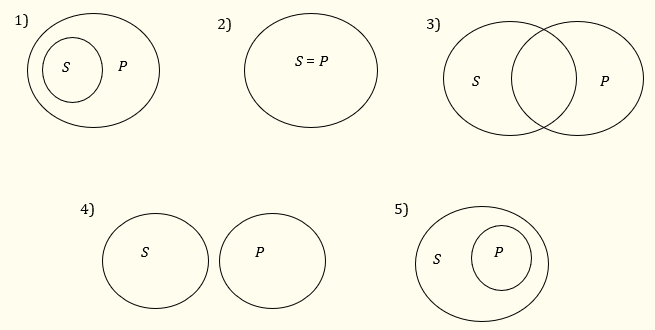
1) отговаря на случая, когато обемът на S е строго подмножество на обема на P. В този случай всички S са P, но не всички Р са S. 2) отговаря на случая, когато обемите на S и на P са едно и също множество. В този случай всички S са P и всички Р са S. 3) представя случая, когато обемите на S и P са пресичащи се множества, но никое от двете не е подмножество на другото. В този случай някои S са P и някои P са S, но не вярно, че всички S са P, нито че всички P са S. 4) отговаря на случая, когато обемите на S и Р са изключващи се множества. Тогава нито едно S не е P и нито едно P не е S. И накрая 5) отговаря на случая, когато обемът на P е строго подмножество на обема на S. В този случай всички Р са S, но не всички S са Р.
Очевидно, едно общо-утвърдително (А) изречение „Всяко S е Р“ е истинно в случаи 1) и 2) и е неистинно в останалите три случая – във всеки от тях има такива S, които не са Р. От друга страна твърдение с формата „Някои S не са Р“ (О-твърдението) е истинно в случаи 3), 4) и 5), защото тогава има някакви S, които не са P, и е неистинно в останалите два случая. Получава се, че А-твърдението е истинно, когато О-твърдението е неистинно, и е неистинно, когато O-твърдението е истинно. С други думи общо-утвърдителното и частно отрицателното твърдение (с един и същи субект и предикат) са точни отрицания едно на друго. Това може да се изрази със следните две логически еквивалентности:
| SaP ⇔ ¬SoP |
| ¬SaP ⇔ SoP |
Все едно е дали ще кажем „Всички хора са благородни“ или „Не е вярно, че някои хора не са благородни“. По същия начин е все едно дали ще кажем „Не е вярно, че всички хора са благородни“ или „Някои хора не са благородни“. Впрочем това ни дава друг начин, различен от стандартната форма, да правим общо-утвърдителни или частно-отрицателни твърдения – като отричаме съответните частно-отрицателни или общо-утвърдителни твърдения.
Диаграмата също така показва, че E-твърдението („Нито едно S не е P“) е истинно в случай 4) и е неистинно във всички останали възможни случаи, докато I-твърдението („Някои S са Р“) е неистинно само в случай 4) и е истинно във всички останали възможни случаи, т.е. Е и I-твърденията също са точни отрицания едно на друго:
| SeP ⇔ ¬SiP |
| ¬SeP ⇔ SiP |
Все едно е дали ще кажем „Нито един човек не е благороден“ или „Не е вярно, че някои хора са благородни“, както е все едно и дали ще кажем „Не е вярно, че нито един човек не е благороден“ или „Някои хора са благородни“. Това ни дава алтернативен начин да правим общо-отрицателни или частно-утвърдителни твърдения – като отричаме съответните частно-утвърдителни или общо-отрицателни твърдения.
Така че налице е определено отношение по истинност между А и 0-твърденията, от една страна, и Е и I-твърденията, от друга (при условие, че субектът и предикатът в тях са едни и същи). Отношението е, че твърденията в двете двойки имат винаги различна истинностна стойност, т.е. едното е точно отрицание на другото. С цел онагледяване на тези и други отношения по истинност между видовете категорични твърдения през Средновековието е създадена диаграмата на така наречения логически квадрат. Това е квадрат, на четирите върха на който по определен начин са разположени четирите категорични твърдения:

Този определен начин е следният: общите твърдения са отгоре, частните – отдолу; утвърдителните са отляво, отрицателните – отдясно. Освен това са начертани диагоналите на квадрата, като по този начин между всеки две твърдения има линия, която отговаря на отношението по истинност между тях.
- Противоречивост
По-горе обсъдихме отношението, отговарящо на двата диагонала: това е отношението на противоречивост или на точно отрицание. То е най-определеното и ясно от всички отношения в логическия квадрат – общо-утвърдителното (А) твърдение и частно-отрицателното (О) твърдение, от една страна, и общо-отрицателното (Е) твърдение и частно-утвърдителното (I) твърдение, от друга, са като скачено съдове – каквато и истинностна стойност да има някое от четирите твърдения, това по диагонала има винаги обратната истинностна стойност.
| От две противоречиви твърдения едното е истинно, а другото е неистинно – те не могат да бъдат едновременно истинни или едновременно неистинни. |
Ако знаем истинностната стойност на произволно категорично твърдение, винаги можем да заключим за истинностната стойност на неговото противоречиво – тя е обратната (неистина, ако първото е истинно, и истина, ако е неистинно).
- Противност
Да разгледаме сега отношението между двете общи твърдения – А и Е, на което отговаря горната страна на квадрата. Ясно е, че ако „Всяко S е P“ е истинно, то „Нито едно S не е P“ не може да е истинно, и обратно – ако нито едно S не е P, не може всяко S да е P. Следователно, ако някое от общите твърдения е истинно, другото общо задължително е неистинно. С други думи от истинността на едното общо твърдение (утвърдителното или отрицателното) може логически да се заключи за неистинността на другото. Не така обаче стоят нещата в посоката от неистинност към истинност. Ако „Всяко S е P“ е неистинно, е възможно нито едно S да не е P (и тогава „Нито едно S не е P“ ще е истинно), но също така е възможно някои S да са P, а други да не са P (и тогава „Нито едно S не е P“ ще е неистинно). Например, ако не е вярно, че всички хора са благородни (ако „Всички хора са благородни“ е неистинно), е логически възможно някой хора да са благородни, а други – да не са (и тогава „Нито един човек не е благороден“ ще е неистинно), но също е възможно да няма благородни хора (и тогава „Нито един човек не е благороден“ ще е истинно). Следователно, ако А-твърдението е неистинно, не може да се каже само на логически основания каква е истинностна стойност на Е-твърдението – то може както да е истинно, така и да е неистинно. Ще изразяваме накратко това положение на нещата, като казваме, че истинностната стойност на E-твърдението е неопределена (логически).
По аналогичен начин се вижда, че нещата в посоката от общо-отрицателното към общо-утвърдителното твърдение стоят по същия начин: ако Е-твърдението е неистинно, истинностната стойност на А-твърдението е неопределена. Ако не е вярно, че нито един човек не е благороден (ако „Нито един човек не е благороден“ е неистинно), е възможно както всички хора да се благородни, така и някои хора да са благородни, а други да не се (в първия случай „Всички хора са благородни“ ще е истинно, а във втория ще е неистинно).
Отношението между двете общи твърдения (на което отговаря горната страна на логическия квадрат) се нарича отношение на противност (А и Е-твърденията са противни едно на друго).
| Две противни твърдения не могат да бъдат едновременно истинни, но могат да бъдат едновременно неистинни. (Също едното може да е истинно, а другото неистинно.) |
- Подчиненост
В традиционната логика се приема, че частните твърдения следват логически от съответните им общи, т.е. частно-утвърдителното следва от общо-утвърдителното и частно-отрицателното следва от общо-отрицателното (когато разбира се субектът и предикатът им са едни и същи). Ако е истинно, че всички хора са благородни, ще е истинно и че някои хора са благородни (т.е. тогава поне един човек ще е благороден), и ако е истинно, че нито един човек не е благороден, ще е истинно и че някои хора не са благородни (поне един човек няма да е благороден). Очевидното (на пръв поглед) основание за това е, че щом нещо е изпълнено за всички елементи на едно множество (в примера множеството на хората), то ще е изпълнено и за част от елементите му. Съществено изискване за това (уж очевидно) основание обаче е въпросното множество да не е празно, защото ако е празно, общото твърдение ще е истинно, а частното неистинно. Причината за това е следната.
Ако няма S-ове, частно утвърдителното и частно-отрицателното твърдение ще са неистинни, защото могат да се перифразират съответно със „Съществува нещо, което е S и което е P“ и „Съществува нещо, което е S и което не е P“. Когато не съществуват каквито и да е S-ове, тези две изречения са очевидно неистинни. В този случай обаче общо-утвърдителното и общо-отрицателното твърдение са истинни, защото могат да се перифразират съответно с „Ако едно нещо е S, то е и P“ и „Ако едно нещо е S, то не е P“. Тези изречения не се ангажират със съществуването на S-ове и съответно не са неистинни, когато такива не съществуват. По този начин, ако множеството на всички S-ове е празно, общите твърдения са истинни, а частните неистинни, което означава, че вторите не следват логически от първите.
В традиционната логика обаче мълчаливо се предпоставя, че когато изказваме някакво общо твърдение (било то утвърдително или отрицателно) обемът на субекта му не е празно множество. Така че в традиционната логика частното твърдение следва логически от общото:
| SaP ⇒ SiP |
| SeP ⇒ SoP |
Това отношение се нарича подчиненост и отговаря на лявата и дясната страна на квадрата в посока отгоре надолу. То е единственото отношение в логическия квадрат, което е представлява логическо следване, т.е. при което от истинността на едно твърдение следва истинността на друго. При останалите отношения е налице заключаване от истинност за неистинност, от неистинност за истинност или от неистинност за неистинност, не и от истинност за истинност.
Ако едно общо твърдение (А или Е) е неистинно, неговото подчинено (съответно I или О) е неопределено (би могло да е както истинно, така и неистинно). Например, ако всичко което знаем за интелигентността на котките е, че е неистинно, че всички котки са интелигентни, то има две възможности – или нито една котка да не интелигентна, в който случай подчиненото („Някои котки са интелигентни“) би било неистинно, или някои котки да са интелигентни, а други да не са, в който случай подчиненото би било истинно. Аналогично стоят нещата и с E и O-твърденията.
- Подпротивност
Частно-утвърдителното (I) и частно-отрицателното (О) твърдение с един и същ субект и предикат се наричат подпротивни едно на друго. Характерно за това отношение, на което отговаря долната страна на квадрата, е, че двете твърдения могат да бъдат едновременно истинни, но не могат да бъдат едновременно неистинни. Да си представим, че някои котки са интелигентни, а други не са. Тогава I-твърдението (“Някои котки са интелигентни”) и О-твърдението (“Някои котки не са интелигентни”) ще бъдат едновременно истинни. От друга страна, ако е неистинно, че някои котки са интелигентни, то нито една котка не е интелигентна и следователно (тривиално) някои котки не са интелигентни. Така че, ако “Някои котки са интелигентни” е неистинно, то подпротивното му “Някои котки не са интелигентни“ е истинно. По подобен начин, в другата посока, ако частно-отрицателното (О) твърдение е неистинно, то подпротивното му (I) твърдение ще е истинно. Така че, в сравнение с противните твърдения, подпротивните се отнасят едно към друго по обратния начин – те могат да бъдат едновременно истинни, но не и неистинни, докато противните могат да бъдат едновременно неистинни, но не и истинни.
Въз основа на отношенията в логическия квадрат, ако знаем истинностната стойност на едно категорично твърдение, можем да заключим за истинностната стойност на всички или на някои от останалите три вида твърдения със същия субект и предикат. За да направим това, не се нуждаем от използването на всички отношения в квадрата. Използването на отношенията по диагоналите (противоречивост) и горната страна на квадрата (противност) e достатъчно за всяко такова заключение. Нека видим защо.
Да приемем, че знаем за някакво частно-отрицателното (О) твърдение, че е истинно, и искаме да определим каква е тогава истинностната стойност на останалите три вида твърдения със същия субект и предикат. По диагонала от отношението на противоречивост следва, че А-твърдението ще е неистинно. Но от отношението на противност между двете общи твърдения знаем, че ако едното (в случая A-твърдението) е неистинно, истинностната стойност на другото (в случая на Е-твърдението) е неопределена (може да е както истинно, така и неистинно). Но тогава ще е неопределена и истинностната стойност на намиращото се по диагонала негово отрицание – О-твърдението. Това е така, защото двете са като скачени съдове, поради което ако истинностната стойност на едното е определена, ще е определена и на другото (ще бъде обратната). Така че, взимайки предвид отношенията на противоречивост и подчиненост, получаваме, че когато О-твърдението е истинно, А-твърдението е неистинно, а истинностните стойности на E и I-твърденията са неопределени (могат да бъдат както И, така и Н).
Да видим сега каква ще е истинната стойност на другите три твърдения, ако истинностната стойност на O-твърдението е Н. По диагонала получаваме, че А-твърдението (отрицанието на О) е истинно. От отношението на противност знаем, че ако едното общо твърдение е истинно, другото общо е неистинно. Значи Е-твърдението е неистинно. Но тогава по диагонала неговото отрицание (I-твърдението) ще е истинно. Като цяло, въз основа на отношенията на противоречивост и противност, получаваме, че когато частно-отрицателното (О) твърдение е неистинно А и I-твърденията са истинни, а Е-твърдението е неистинно.
По напълно аналогичен начин, ако знаем истинностната стойност на едно от четирите категорични твърдения, чрез използване на отношенията на противоречивост, противност и подчиненост можем да определяме истинностната стойност на останалите три твърдения (в случай, че това е възможно). По принцип винаги се получава или че истинностната стойност на едното от тях (на това по диагонала) е определена, а на другите две е неопределена (както беше, когато О-твърдението е истинно), или че истинностната стойност и на трите е определена (както беше, когато О-твърдението е неистинно).
Това изчерпва съдържанието на логическия квадрат. Двете най-важни неща в него, които ще използваме и по-нататък, са 1) че общо-утвърдителното (А) и частно-отрицателното (О) твърдение, от една страна, и общо-отрицателното (Е) и частно-утвърдителното (I) твърдение, от друга, са точни отрицания едно на друго, поради което винаги имат обратната истинностна стойност, и 2) че (според разбирането на традиционната логика) частно-утвърдителното (I) твърдение следва логически от общо-утвърдителното (A), а частно-отрицателното (О) – от общо-отрицателното (Е), т.е. от едно общо твърдение следва частното със същото качество.
Долната таблица обобщава отношенията между твърденията в логическия квадрат.
| Ако едно твърдение е | истинно | неистинно |
| неговото противоречиво е | неистинно | истинно |
| неговото противно е | неистинно | неопределено |
| неговото подчинено е | истинно | неопределено |
| неговото подпротивно е | неопределено | истинно |
Задачи
(Изтеглете задачите като pdf.)| (1) Каква е истинностната стойност на останалите три вида категорични твърдения, ако: |
| 1) | общо-утвърдителното е истинно. |
| 2) | общо-утвърдителното е неистинно. |
| 3) | общо-отрицателното е истинно. |
| 4) | общо-отрицателното е неистинно. |
| 5) | частно-утвърдителното е истинно. |
| 6) | частно-утвърдителното е неистинно. |
| (2) Ако приемем, че долните твърдения са истинни, какво можем да заключим за истинностните стойности на останалите три вида твърдения със същия субект и предикат? |
| 1) | Някои известни актьори са много интелигентни хора. |
| 2) | Нито едно животно с рога не е хищник. |
| 3) | Всички изотопи на урана са много нестабилни субстанции. |
| 4) | Някои добри писатели не са увлекателни лектори. |
1. Във всеки от показаните случаи се предпоставя, че S и Р не са празни, т.е. че има някакви неща, които попадат под тях. Тази предпоставка се прави (мълчаливо) в традиционната логика. Ще говорим за това по-нататък – виж 2.6 Диаграми на Вен. ↩

