4. Некласически логики
Класическата (модерна) логика се състои от пропозиционалната и предикатната логика. Некласическите логики са или разширения, или алтернативи на класическата логика. Първите я разширяват, като обогатяват езика ѝ, а вторите отхвърлят някои нейни основни принципи, замествайки ги с други. Семейството на некласическите логики е голямо. В тази част накратко ще разгледаме две от най-важните групи некласически логики – модалните и тризначните логики.
4.1 Модални логики
Модалните оператори и връзката между тях
Модалната логика е разширение на класическата пропозиционална и предикатна логика, което се получава, като към техния символен език се добавят така наречените модални оператори. Модалните оператори обикновено са два и за тях се използват символите „□“ и „◊“. В зависимост от семантиката на съответната модална логика модалните оператори имат различно значение – „необходимо“ и „възможно“; „задължително“ и „позволено“; „винаги е било“ („винаги ще бъде“), „някога е било“ („някога ще бъде“) и други.
Алетичната1 модална логика е най-старата от модалните логики и често, когато се говори за модална логика, се има предвид именно тя. В нея операторът „□“ има смисъла на „по необходимост“ или „необходимо е“, а оператора „◊“ – на „възможно е“. Например изречението „По необходимост всяко нещо е идентично със себе си“ би могло да се представи символно с „□∀x(x=x)“, а изречението „Възможно е Париж да не беше столица на Франция“ – с „◊¬Fab“, където „a“ отговаря на „Париж“, „b“ – на „Франция“ и „F“ – на предиката „…е столица на…“.
В деонтичната модална логика операторът „□“ се интерпретира като „задължително е“, „трябва“, а „◊“ – като „позволено е“, „допустимо е“, „може“. Например изречението „Добрият самарянин е длъжен да помогне на ранения на пътя“ би могло да се представи в нейната символика с „□Fab“, където „a“ и „b“ отговарят на „добрия самарянин“ и „ранения на пътя“, а „F“ – на двуместния предикат „…помага на…“. Изразът „◊¬Fab“ тогава би представял символно изречението „Допустимо е добрият самарянин да не помогне на ранения на пътя“. „Забранено е“ се представя или с „¬◊“ („не е позволено“), или с „□¬“ („задължително е да не“).
В темпоралната модална логика има две двойки модални оператори – една за бъдещето и една за миналото. Ако използваме индексите „p“ и „f“ съответно за „минало“ („past“) и „бъдеще“ („future“), „□p“ ще отговаря на „винаги е било“, „◊p“ – на „някога е било“, „□f“ – на „винаги ще бъде“ и „◊f“ – на „някога ще бъде“. Тогава, ако „a“ отговаря на „Сократ“, формулата „□f ◊p∃x x=a“ ще представя символно истинното изречение „Сократ винаги ще е съществувал“. Изречението е истинно, защото „∃x x=a“ има смисъла на „Съществува нещо, което е идентично със Сократ“, което е еквивалентно на „Сократ съществува“. Следователно, смисълът на „◊p∃x x=a“ е „Имало е момент в миналото, в който Сократ е съществувал“, или накратко „Сократ е съществувал“. Съответно смисълът на „□f ◊p∃x x=a“ е „Винаги ще е факт, че Сократ е съществувал“, или накратко „Сократ винаги ще е съществувал“. По подобен начин може да се види, че „◊f □p∃x x=a“ представя символно неистинното изречение „Ще има момент, в който Сократ винаги ще е съществувал“.
В епистемичната модална логика „□“ се интерпретира като „вярва, че...“ или „знае, че...“. Знанието и вярването са свързани с някакъв (знаещ или вярващ) субект, поради което в епистемичната модална логика към всеки модален оператор има индекс, който обозначава субекта, за който се говори (например „□n“, „◊n“ и т.н.). Нека интерпретираме „□n“ като „n знае, че“. Ако „a“ представя символно „Сократ“, а „b“ – „Бог“, „□a∃x x=b“ ще представя символно изречението „Сократ знае, че Бог съществува“. Ако въпросната епистемична модална логика отново се отнася до знанието, а не до вярването, смисълът на другия модален оператор („◊n“) може да се предаде с думите „знанието на n не изключва, че …“ или със „според n е възможно … да е факт“. Тогава „◊a∃x x=b“ представя символно изречението „според Сократ Бог може и да съществува“.
Ще наричаме „□“ и „◊“ съответно „силен“ и „слаб“ модален оператор. Независимо от вида на модалната логика (дали е алетична, деонтична, темпорална или епистемична) между изразите, отговарящи на силния и на слабия модален оператор, съществува логическа връзка, аналогична на връзката между кванторите в предикатната логика. Също както при тях тази връзка позволява единият от двата модални оператора да се изрази чрез другия. Нека я разгледаме.
Да приемем първо, че „□“ и „◊“ се интерпретират съответно като „необходимо“ и „възможно“. Тогава „¬□α“ ни казва „α не е необходимо“ (например „Не е необходимо вселената да е безкрайна“). Но това е все едно да се каже „Възможно е не-α“ („◊¬α“) („Възможно е вселената да не е безкрайна“). Така че между модалните оператори в алетичната модална логика съществува еквивалентност, аналогична на еквивалентността между „¬∀xα“ и „∃x¬α“ в предикатната логика:
| ¬□α ⇔ ◊¬α |
В деонтичната модална логика на „¬□α“ отговаря изречението „Не е задължително α“. То има същия смисъл като на „Позволено е не-α“ („◊¬α“). Ако не съм длъжен да направя нещо, значи е позволено да не го направя, и обратно – ако е позволено да не направя нещо, не съм длъжен да го направя. Следователно същата еквивалентност важи и в деонтичната модална логика.
Еквивалентността е налице също в темпоралната модална логика по отношение и на двете двойки модални оператори – за миналото и за бъдещето. „¬□pα“ отговаря на изречението „Не винаги е било α“, което има същия смисъл като изречението „Някога е било не-α“ („◊p¬α“). (Ако Земята не винаги е съществувала, то някога Земята не е съществувала, и обратно.) По същия начин изречението „Не винаги ще е истинно α“ („¬□f α“) има същия смисъл като изречението „Някога няма да е истинно α“ („◊f ¬α“) (Ако Земята не винаги ще съществува, ще дойде момент, в който Земята няма да съществува, и обратно).
Тъй като „α“ стои на мястото на произволно изречение, ако го специфицираме като произволно отрицание (т.е. ако заместим „α“ с „¬α“), от горната еквивалентност („¬□α“ ⇔ „◊¬α“) получаваме еквивалентността „¬□¬α“ ⇔ „◊¬¬α“, от която, като махнем двойното отрицание, получаваме схема еквивалентност, чрез която слабият модален оператор може да бъде дефиниран чрез силния и отрицанието:
| ¬□¬α ⇔ ◊α |
Тази схема еквивалентност се потвърждава и от интуицията: да не е необходимо не-α е същото като да е възможно α; да не съм длъжен да не направя нещо е същото като да ми е позволено да го направя; да не е вярно, че винаги в миналото нещо не е било факт е същото като в някакъв минал момент то да е било факт; да не е вярно, че винаги в бъдещето нещо няма да е факт е същото като в някакъв бъдещ момент то да стане факт.
От логическата еквивалентност между „¬□¬α“ и „◊α“ следва, че отрицанията им „¬¬□¬α“ и „¬◊α“ също ще бъдат еквивалентни, и тъй като „¬¬□¬α“ е същото като „□¬α“, получаваме следната еквивалентност:
| □¬α ⇔ ¬◊α |
По необходимост нещо да не е факт е същото като това нещо да не е възможно; да съм длъжен да не правя нещо е същото като да не ми е позволено да го правя; нещо винаги да не е било истинно е същото като да не е вярно, че някога е било истинно; по същия начин и за бъдещето.
Накрая, замествайки в горната еквивалентност α с „¬α“ и махайки двойното отрицание, получаваме четвърта връзка между модалните оператори, която позволява „□“ да бъде изразено чрез „◊“ и отрицанието:
| □α ⇔ ¬◊¬α |
Все едно е да се каже, че нещо е необходимо, или че отрицанието му не е възможно; както и да се каже, че някой е длъжен да направи нещо, или че не му е позволено да не го направи; както и че нещо винаги е било факт, или че е нямало момент, в който не е било факт; по същия начин и за бъдещето.
Следната таблица обобщава връзката между силния и слабия модален оператор:
| ¬□α ⇔ ◊¬α | ¬□¬α ⇔ ◊α | □¬α ⇔ ¬◊α | □α ⇔ ¬◊¬α |
| Алетична | |||
|
не е необходимо ⇕ възможно е да не е |
не е необходимо да не е ⇕ възможно е |
по необходимост не е ⇕ не е възможно |
необходимо е ⇕ не е възможно да не е |
| Деонтична | |||
|
не е задължително ⇕ позволено е да не |
не е задължително да не ⇕ позволено е |
задължително не ⇕ не е позволено |
задължително е ⇕ не е позволено да не |
| Темпорална | |||
|
не винаги е било ⇕ някога не е било |
не винаги не е било ⇕ някога е било |
винаги не е било ⇕ не е вярно, че някога е било |
винаги е било ⇕ не е вярно, че някога не е било |
|
не винаги ще бъде ⇕ някога няма да бъде |
не винаги няма да бъде ⇕ някога ще бъде |
винаги няма да бъде ⇕ не е вярно, че някога ще бъде |
винаги ще бъде ⇕ не е вярно, че някога няма да бъде |
От това, че връзката между модалните оператори е напълно аналогична на връзката между кванторите, следва, че модалните оператори ще се държат точно като кванторите, когато е налице поредица от оператори, от едната страна на които има отрицание. Тогава отрицанието може да мине от другата страна на поредицата, като всеки от операторите се обърне (силният стане слаб и обратно). Наприме𠄬□□◊□“ има същия смисъл като „◊◊□◊¬“.
Синтаксис на модалната логика
Единствената разлика между символните езици на модалните логики и тези на класическата пропозиционална или предикатна логика е, че в първите има два допълнителни символа – модалните оператори „□“ и „◊“. (В темпоралната модална логика операторите са четири – „□p“, „◊p“, „□f“ и „◊f“). От синтактична гледна точка модалните оператори се държат точно като логическия съюз на отрицанието – също като него те се слагат в началото на произволна формула α, в резултат на което се получава нова формула – „□α“ или „◊α“. В предишната подсекция видяхме, че зависимост от вида на модалната логика „□α“ изразява различни неща – „ необходимо е α“, „задължително е α“ и т.н., но това вече е въпрос на семантика, а не на синтаксис.
За строгото формулиране на синтаксиса на модалната пропозиционална логика както и на синтаксиса на модалната предикатна логика е достатъчно към синтактичните правила съответно на пропозиционалната логика (виж) и на предикатната логика (виж) да се добави следното едно-единствено синтактично правило:
| Ако α е правилно-образуван израз (формула), то □α и ◊α също са правилно-образувани изрази (формули).2 |
С помощта на това ново правило и останалите синтактични правила можем да заключим например, че „□∀x(Fxa → ◊¬◊Gx)“ е правилно образуван израз (формула) на модалната предикатна логика и че например „∃x□(Fxa → ◊Gx ∨ Ha)“ не е такъв, както и че например „□(¬p → ◊¬□q)“ е правилно-образуван израз на модалната пропозиционална логика, докато „□(p → ◊q ∨ ¬r)“ не е.
Семантика на модалната логика
Факторите, които определят дали едно твърдение е истинно, или неистинно, са две. Единият е неговото значение, което зависи от значението на думите и изразите, от които е съставено, а другият е положението на нещата в света. Да вземем като пример изречението „Земята е планета“. То е истинно и истинността му е обусловена, първо, от значението на думите в него – от това, че думата „Земята“ (за разлика например от думата „Сократ“) обозначава планетата Земя, и от това, че предикатът „...е планета“ е истинен за планетите. Ако значението на думата „Земята“ беше същото, но значението на думата „планета“ беше такова, че тя беше истинна не за планетите, а например за тези и само тези неща, които имат правоъгълна форма, твърдението щеше да е неистинно. Вторият фактор, обуславящ истинността на твърдението, е, че положението на нещата в света е такова, че Земята е планета. Ако положението на нещата беше различно, то можеше да неистинно, дори ако думите, от които е съставено, имаха същото значение.
Интерпретирането на нелогическите символи в пропозиционалната или предикатната логика („p“, „q“, … и т.н. – с твърдения; „F“, „G“, … и т.н. – с предикати; „a“, „b“, … и т.н. – с единични термини) фиксира единия от двата фактора – значението, докато другия, положението на нещата в света, класическата логика оставя такова, каквото си е. Когато значението на символите е фиксирано посредством интерпретацията им, вторият фактор, положението на нещата в света, автоматично определя истинностните стойности на формулите. Така че в класическата логика интерпретацията на изразите варира, докато положението на нещата в света е постоянно. Напротив в модалната логика варира и вторият фактор, тъй като тя разглежда различни алтернативни положения на нещата в света. Нуждата за това се корени в самите модални понятия. Нека видим защо.
Едно изречение от вида „Възможно е α“ може да е истинно, въпреки че изречението α е неистинно. Например изречението „Възможно е София да не беше столица на България“ е истинно (това действително е логически възможно), въпреки че София е столица на България. По същия начин едно изречение от вида „Необходимо е α“ може да е неистинно, въпреки че α е истинно. Например „София е столица на България по необходимост“ е неистинно изречение, въпреки че изречението „София е столица на България“ е истинно. Причината за разликата в истинностните стойности на α, от една страна, и „□α“ и „◊α“, от друга, е, че истинностните стойности на последните зависят не само от положението на нещата в света, но също и от положението на нещата в други, алтернативни възможни светове. За да е истинно изречението „Възможно е α“, е достатъчно да има поне един възможен свят, в който изречението α да е истинно, дори и α да е неистинно в действителния свят. „Възможно е София да не беше столица на България“ е истинно изречение, защото можем да си представим различен от нашия възможен свят, в който София не е столица на България. По същия начин, за да е истинно изречението „Необходимо е α“, не е достатъчно α да е фактически истинно, то трябва да е истинно във всеки възможен свят. Твърдението „София е столица на България по необходимост“ е неистинно, защото, въпреки че София е столица на България, можем лесно да си представим възможни светове, в които това не е така.
В семантиката на класическата (пропозиционална или предикатна) логика изреченията получават истинностна стойност единствено по отношение на действителното положение на нещата, т.е. само с оглед на актуалния, действителен свят, поради което там изобщо не се говори за възможни светове. Напротив, семантиката на модалната логика често се нарича „семантика на възможните светове“, защото, за да получат истинностна стойност изреченията от вида „Необходимо е α“ и „Възможно е α“, изречението α трябва да получи истинностна стойност във всеки възможен свят – всъщност във всеки възможен свят от едно множеството от възможни светове, за което си представяме, че е множеството на всички възможни светове. Ще означаваме това множество с „W“. W може да различно в различните контексти. Едно изречение от вида „Необходимо е α“ има стойност И в който и да е възможен свят от W (нашият, действителен свят е само един от тях), ако и само ако α има стойност И във всеки свят от W. Съответно, едно изречение от вида „Възможно е α“ има стойност И в който и да е възможен свят от W, ако и само ако α има стойност И в поне един свят от W. Така че следното семантично правило е базово за модалните логики:
| (1) | □α има стойност И в който и да е възможен свят от W, ако и само ако α има стойност И във всеки свят от W. |
| ◊α има стойност И в който и да е възможен свят от W, ако и само ако α има стойност И в поне един свят от W. |
Прибавяйки това семантично правило към семантичните правила на класическата пропозиционална или предикатна логика получаваме една определена семантика съответно за модалната пропозиционална или модалната предикатна логика. Важна разлика между класическата семантика и семантиката на модалната логика е, че при първата изреченията получават истинностна стойност сами по себе си, докато при втората получават истинностна стойност винаги по отношение на някакъв възможен свят от W. Действителният свят е само един от тях.
Няколко думи за понятието за възможен свят. За възможните светове можем да мислим като за максимално определени възможни положения на нещата. Като правило едно възможно положение на нещата не е максимално определено. Възможно положение на нещата е например това, София да не е столица на България. То е донякъде определено по отношение на това, коя е столицата на България, но не е определено по отношение на всичко останало. Можем да увеличим определеността му като добавим например, че в него снегът е бял. Можем да продължим да го определяме, казвайки например, че (за разлика от действителното положение на нещата) в него Пловдив е по-голям град от София и т.н., и т.н. За да се превърне във възможен свят, това положение на нещата трябва да стане максимално определено. С други думи в един възможен свят за всяко твърдение трябва да е определено дали е истинно в него, или не.
По същество семантиката на възможните светове дефинира понятието за необходимост като истинност във всеки възможен свят, а понятието за възможност – като истинност в поне един възможен свят. Това показва откъде идва пълната аналогия между връзката между кванторите (синонимността на „¬∀x“ и „∃x¬“, „∀x¬“ и „¬∃x“ и т.н.) и връзката между модалните оператори (синонимността на „¬□“ и „◊¬“, „□¬“ и „¬◊“ и т.н.). Модалните оператори са всъщност квантори, които квантифицират не нещата от света (универсума на дискурса), а възможните светове от множеството на всички възможни светове. Посредством универсалния квантор утвърждаваме, че нещо е истинно за всеки обект от универсума на дискурса, а чрез силния модален оператор (оператора за необходимост в алетичната модална логика) утвърждаваме, че нещо е истинно във всеки свят от множеството на всички възможни светове. По същия начин посредством екзистенциалния квантор утвърждаваме, че нещо е истинно за поне един обект от универсума на дискурса, а чрез слабия модален оператор (този за възможност в алетичната модална логика), че нещо е истинно в поне един свят от множеството на всички възможни светове.
От класическата логика знаем, че понятията за логическо следване и логическа еквивалентност се свеждат до понятието за логическа валидност (виж): от α логически следва β, когато „α→β“ е логически валиден израз (тавтология); и α е логически еквивалентно на β, когато „α↔β“ е логически валиден израз. Така че, за да дефинираме понятията за логическо следване и логическа еквивалентност, е достатъчно да дефинираме понятието за логическа валидност. В семантиката на модалните логики последното се дефинира така:
| Една формула е логически валидна, ако и само ако независимо от това, кое е множеството на възможните светове W и как интерпретираме нелогическите ѝ символи („p“, „F“, „a“ и т.н.), тя e винаги истинна във всеки свят от W. |
За простота (а и тъй като семантиката ѝ е по-безпроблемна) ще се придържаме към модалната пропозиционална логика. Нелогическите символи в нейния символен език са буквите за твърдения „p“, „q“, „r“... Интерпретацията им в даден възможен свят се състои в това, да се определят истинностните им стойности. Определянето на последните идва от интерпретирането на буквите за твърдения с някакви прости (от гледна точка на пропозиционалната логика) твърдения, които са или истинни, или неистинни в въпросния възможен свят. Според дефиницията за логическа валидност от предишния параграф дадена формула ще е логически валидна, ако независимо кое е множеството на възможните светове W и независимо какви истинностни стойности даваме на буквите за твърдения в различните възможни светове, във всеки от тях формулата ще получава стойност И.
Всеки израз с формата на тавтология ще е логически валиден за семантиката на модалната логика. Например, каквато и формула да е α, формулата „α→α“ ще е логически валидна, защото независимо от истинностната стойност на α в даден възможен свят „α→α“ ще има стойност И в него. Това показва, че „α→α“ има стойност И във всеки свят от всяко множество от възможни светове, независимо какви са истинностните стойности на буквите за твърдения, участващи в α, в различните възможни светове, т.е. изразът е логически валиден според дефиницията. В „α→α“ може да участват и модални оператори. Това не променя горното разсъждение – важно е изразът да има като цяло формата на тавтология; не е нужно непременно да е формула на пропозиционалната логика.
Логически валидни в модалната пропозиционална логика са и много други формули, които нямат формата на тавтологии, но чиято валидност е свързана с модалните оператори. Ще въведем метод, чрез който ще можем да проверяваме дали даден модален израз е логически валиден. Методът използва диаграми и допускане на противното и работи по следния начин. За да проверим дали дадена модална формула е логически валидна, допускаме, че не е валидна, т.е. – че в някакъв възможен свят при някакво даване на истинностни стойности на буквите ѝ за твърдения получава стойност Н, и започваме да правим изводи от това допускане. Ако стигнем до противоречие, с това ще докажем, че допускането не е възможно, което означава, че формулата е истинна във всеки свят от всяко множество от възможни светове при всяко даване на истинностни стойности на буквите й твърдения, т.е. че е логически валидна. Ако не стигнем до противоречие, рано или късно ще стигнем до модел на отрицанието на формулата, т.е. ще намерим конкретно множество от възможни светове и възможен свят в него, в който формулата има стойност Н за някакви конкретни стойности на буквите ѝ за твърдения. Това би доказало, че формулата не е логически валидна.
Ето един пример. Долната диаграма е доказателство, че всяка формула от вида „□α→α“ („Ако нещо е необходимо, то е факт“) е логически валидна, т.е., че от „□α“ логически следва α.
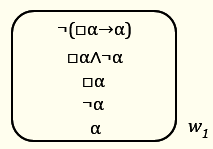
Правоъгълникът отговаря на някакъв свят от някакво множество от възможни светове W, който сме означили с „w1“. Допуснали сме, че изразът „□α→α“ е неистинен в този свят. Тогава отрицанието му е истинно в него, поради което на първия ред сме написали „¬(□α→α)“. По конвенция изреченията, които пишем в правоъгълника на даден свят, са истинни в него. Вторият израз е логически еквивалентен на първия по материална импликация3, така че и той трябва да е истинен в w1. От истинността на „□α∧¬α“ по симплификация следва истинността на „□α“ и „¬α“ в w1 (третия и четвъртия ред). Тъй като изречението „□α“ („Необходимо е α“) е истинно в w1, въз основа на въведеното по-горе семантично правило (1) следва, че α е истинно във всеки възможен свят от W и значи също и в w1, поради което на най-долния ред сме написали „α“. α обаче противоречи на „¬α“. Тъй като в никой възможен свят не може да има противоречие, началното допускане (че има множество от възможни светове и свят в него, в който „□α→α“ е неистинно) е невъзможно. Следователно, всяка формула от вида „□α→α“ е логически валидна.
Като следващ пример ще покажем логическата валидност на формулите от вида „□α→□□α“, т.е. ще покажем, че от това, че нещо е необходимо, следва, че то е необходимо с необходимост. Следната диаграма е доказателство за това:

Започваме с допускането, че в някакъв възможен свят w1 е истинно отрицанието на „□α→□□α“, от което, както в предишния пример, се получава, че „□α“ и „¬□□α“ са истинни в w1. Въз основа на връзката между модалните оператори „¬□“ в „¬□□α“ може да бъде заместено с „◊¬“, в резултат на което получаваме, че „◊¬□α“ е истинно в w1. Щом „◊¬□α“ е истинно в w1, от семантичното правило (1) следва, че трябва да съществува възможен свят (да го наречем „w2“), в който „¬□α“ е истинно. Затова сме начертали втори правоъгълник за света w2 и най-отгоре в него сме написали „¬□α“. От връзката между модалните оператори „¬□α“ е еквивалентно на „◊¬α“, така че „◊¬α“ е истинно в w2. Въз основа на семантичното правило (1) истинността на „◊¬α“ в w2 ни дава право да заключим, че съществува възможен свят (да го наречем „w3“), в който „¬α“ е истинно. Съответно сме начертали нов правоъгълник и сме написали „¬α“ най-отгоре в него. В w1 обаче е истинно „□α“, от което въз основа на семантичното правило (1) следва, че във всеки възможен свят трябва да е истинно α. В частност α трябва да е истинно и в света w3, което противоречи на истинността на „¬α“ там. Стигнахме до противоречие. Това завършва доказателството за логическата валидност на „□α→□□α“.
Във въведения метод има нещо много подобно на доказателствената процедура в предикатната логика (виж 3.5 Доказателствена процедура). Там използвахме екзистенциални инстанциации, за да въвеждаме нови индивидни константи, и след това прилагахме универсални инстанциации върху тях. По подобен начин във въведения диаграмен метод истинността на „◊α“ в даден свят ни позволява да въвеждаме нови светове, в който α е истинно, след което истинността на „□β“ в който и да е свят ни дава право да заключаваме за истинността на β във въведените светове. Това подобие на функционирането на двете доказателствени процедури не е случайно. Вече видяхме, че силният и слабият модален оператор се държат като квантори върху множеството на всички възможни светове.
Семантиката, която получаваме посредством семантичното правило (1), не е единствената семантика на модалната логика. Това е най-простата семантика, за която обикновено се смята, че отговаря най-добре на алетичните модалности, т.е. на понятията за необходимост и възможност, но дори и в алетичната модална логика има други семантики, по отношение на които някои от логически валидните изрази за въведената семантика спират да бъдат валидни, а други, които не са валидни за нея, стават валидни. Освен това тази семантика не е подходяща за деонтичната и за темпоралната модални логики.
Семантичното правило (1) може да бъде генерализирано, така че да стане приложимо към всички семантики на модалната логика. Това става като се въвежда така наречената релация на достижимост (accessibility relation), която ще обозначаваме с „R“. Това е някакво отношение между два възможни светове, на което засега не е нужно да даваме определен смисъл. Единственото, което ще предпоставим, е, че някои възможни светове се намират в тази релация към други възможни светове или към самите себе си, а други не. Когато един свят се намира в релацията на достижимост към друг свят, за втория ще казваме, че е достижим от първия. Ще изменим семантичното правило (1) по следния начин, така че да взима предвид релацията на достижимост. „□α“ ще е истинно в даден възможен свят w1 не просто, когато α е истинно във всеки възможен свят, а когато е истинно във всеки достижим от w1 възможен свят; съответно „◊α“ ще е истинно в света w1 не просто, когато съществува възможен свят, в който α е истинно, а когато съществува достижим от w1 възможен свят, в който α е истинно. Ето го и самото генерализирано семантично правило:
| (2) | □α има стойност И в който и да е възможен свят w1 от W, ако и само ако α има стойност И във всеки достижим от w1 свят във W (т.е. във всеки свят w, за който е изпълнено w1Rw). |
| ◊α има стойност И в който и да е възможен свят w1 от W, ако и само ако α има стойност И в поне един достижим от w1 свят във W (т.е. в поне един свят w, за който е изпълнено w1Rw). |
Семантичното правило (1) е частен случай на горното правило, защото (1) се получава от (2), когато релацията на достижимост R е такава, че всеки възможен свят от W се намира в R към всеки свят от W (включително и към самия себе си). Тогава релацията не ограничава световете, в които да се гледа истинността на α, за да са се определи истинността на „□α“ или на „◊α“ в даден свят – това са всички светове от W. Поради това в първото семантично правило изобщо не се говори за релация на достижимост.
В „3.5 Доказателствена процедура“ стана дума за формалните свойства на отношенията (релациите); свойства като рефлексивност, симетричност, транзитивност и т.н. Ето едно друго такова формално свойство. Ако в дадено множество една релация е такава, че всеки елемент от множеството се намира в нея с всеки елемент от множеството (включително и със самия себе си), за релацията се казва, че притежава свойството универсалност в това множество. Следователно, семантичното правило (1) се получава от семантичното правило (2), когато релацията на достижимост R е универсална в множеството на възможните светове W.
Приписвайки различни формални свойства на релацията на достижимост, получаваме различни семантики, които определят по различен начин кои изречения са логически валидни, и кои не. Например, за да са валидни всички изречения от вида „□α→α“, релацията на достижимост R трябва да е рефлексивна; за да са валидни изреченията от вида „□α→□□α“, R трябва да е транзитивна; и т.н. По-горе доказахме, че и двата вида изречения са логически валидни, защото всъщност предпоставяхме, че R е универсална (че всеки свят е достижим от всеки). Когато една релация е универсална, тя задължително също е рефлексивна и транзитивна. Ако обаче R е рефлексивна, но не транзитивна, „□α→α“ ще продължи да е логически валидно, но не и „□α→□□α“. Обратно, ако R е транзитивна, но не рефлексивна, вторият вид изречения ще бъдат логически валидни, но не и първият.
Може да се докаже, че когато R е универсална, логически валидните изречения са точно същите както когато R е едновременно рефлексивна, транзитивна и симетрична. Последният вид релации се наричат релации на еквивалентност. Универсалната релация на достижимост и тази, която е релация на еквивалентност, определят една и съща семантика на модалната логика, въпреки че двете формални свойства не са еквивалентни: всяка универсална релация е релация на еквивалентност, но не и обратното – някои релации на еквивалентност не са универсални.
Определянето на дадена семантика на модалната пропозиционална логика посредством определяне на формалните свойства на релацията на достижимост води до определянето на едно безкрайно множество от логически валидни формули за тази семантика. Можем да мислим за тези множества от формули като за определени системи на модалната логика. По исторически причини някои от тях са получили собствени имена.
Множеството от всички логически валидни формули, когато релацията на достижимост е релация на еквивалентност (или универсална релация), се нарича S5.
Множеството от всички логически валидни формули, когато релацията на достижимост e рефлексивна и транзитивна (но не е задължително симетрична) се нарича S4. S4 е правилно подмножество4 на S5. Причината е, че всяка логически валидна формула при транзитивна и рефлексивна релация на достижимост е логически валидна и когато релацията на достижимост е релация на еквивалентност (универсална релация), но не и обратното. Например изречение от вида „◊α→□◊α“ е логически валидно при универсална релация на достижимост, но не е логически валидно при рефлексивна и транзитивна, но не и симетрична, релация на достижимост.
Долната диаграма показва защо изразът „◊α→□◊α“ („Ако нещо е възможно, то е възможно по необходимост“) е логически валиден само ако релацията на достижимост е симетрична.

Допуснали сме, че „◊α→□◊α“ е неистинно в w1, от което (по материална импликация) следва, че там са истинни „◊α“ и „¬□◊α“. От връзката между модалните оператори последният израз е еквивалентен на „◊□¬α“ („¬□◊α“ е еквивалентен на „◊¬◊α“, който е еквивалентен на „◊□¬α“). От истинността на „◊α“ в w1 следва, че съществува достижим от w1 възможен свят w2, в който α е истинно. По принцип, със стрелка изразяваме, че даден свят е достижим от друг. Това, че от правоъгълника на w1 има стрелка към този на w2, означава, че w2 e достижим от w1. От истинността на „◊□¬α“ в w1 следва, че съществува достижим от w1 възможен свят w3, в който е истинно „□¬α“. От тук нататък, за да успеем да стигнем до противоречие, е нужно да използваме формалните свойства симетричност и транзитивност на релацията на достижимост R. От симетричността на R следва, че след като w3 е достижимо от w1, то и w1 е достижимо от w3. На това отговаря стрелката, която сме поставили в посока от w3 към w1. Тъй като w3 се намира в R към w1, а w1 от своя страна се намира в R към w2, от транзитивността на R следва, че също и w3 се намира в R към w2. Поради това сме сложили стрелка от w3 към w2. Но щом w2 е достижим от w3, от истинността на „□¬α“ в w3 следва, че в w2 ще е истинно „¬α“, което противоречи на истинността на α в w2. Стигнахме до противоречие, което показва, че всеки израз от вида „◊α→□◊α“ е логически валиден, ако релацията на достижимост е симетрична и транзитивна (а значи и ако е универсална или е релация на еквивалентност).
Множеството от всички логически валидни формули, когато релацията на достижимост е рефлексивна и симетрична (но не е задължително транзитивна), се нарича B. Също както S4, B е правилно подмножество на S5. S4 и B са две пресичащи се множества, но никое не е подмножество на другото – „□α→α“ например принадлежи и на двете, „□α→□□α“ – само на S4, a „α→□◊α“ – само на В.
Долната диаграма показва защо изреченията от вида „α→□◊α“ („Ако нещо е факт, то по необходимост е възможно“) са логически валидни само ако релацията на достижимост е симетрична.
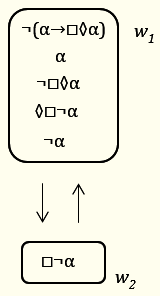
Допускайки, че „α→□◊α“ е неистинно в някакъв възможния свят w1, по материална импликация сме извели, че α и „¬□◊α“ са истинни в него. От връзката между модалните оператори последният израз е логически еквивалентен на „◊□¬α“. Истинността на „◊□¬α“ в w1 ни дава правото да заключим, че съществува достижим от w1 възможен свят w2, в който е истинно „□¬α“. Стрелката надолу изразява, че w2 е достижим от w1. Ако не предпоставим, че релацията на достижимост R е симетрична, ще спрем до тук, без да успеем да стигнем до противоречие. От симетричността на R обаче следва, че щом w1 се намира в R към w2, то и w2 се намира в R към w1. Тогава, тъй като „□¬α“ е истинно в w2, в w1 ще е истинно „¬α“, което противоречи на истинността на α в w1. С това доказахме, че всяко изречение от вида „α→□◊α“ е логически валидно, ако релацията на достижимост е симетрична.
Когато релацията на достижимост е рефлексивна, всеки възможен свят е достижим от самия себе си. Тогава от правоъгълника на всеки свят би трябвало да чертаем извита стрелка водеща към самия него. Първото използване на диаграмния метод по-горе беше при доказателството на валидността на схемата „□α→α“. В това доказателство мълчаливо предпоставихме, че релацията на достижимост е рефлексивна (всъщност, че е универсална, което включва рефлексивността), защото от истинността на □α в w1 заключихме, че α е истинно в w1. Такова заключение обаче е оправдано само при условие, че w1 е достижимо от самото себе си.
Множеството от всички логически валидни формули, когато не налагаме никакви условия на релацията на достижимост, се нарича K. К е правилно подмножество на всяка от горните системи. Никои от споменатите по-горе логически валидни формули (освен тавтологиите) не принадлежи на K. Към K принадлежат например формулите от вида „□(α→β)→(□α→□β)“ – те са логически валидни, без да се налагат никакви условия на релацията на достижимост.
Споменатата историческа причина за имената на горните множества или системи е, че от началото на възникването на модалната логика в началото на 20-ти век до към средата му семантиката на възможните светове не съществува и модалната логика се развива само под формата на различни аксиоматични системи. Горните имена са всъщност имената на въпросните аксиоматични системи. През 60-те години, когато възниква семантиката на възможните светове с релацията на достижимост между тях ((Hintikka, 1961), (Kripke, 1963a, 1963b)), се оказва, че ако налагаме определени формални условия на релацията на достижимост, логически валидни по отношение на получаваните по този начин семантики стават точно тези формули, които преди са били изводими във формулираните по-рано аксиоматични системи!
Що се отнася до деонтичната, темпоралната и епистемичната модални логики. Техните семантики също се получават чрез налагане на определени комбинации от формални свойства върху релацията на достижимост. Например (при стандартното разбиране за време) релацията на достижимост в семантиката на темпоралната модална логика би трябвало да е транзитивна и aсиметрична, докато в семантиката на деонтичната модална логика би трябвало да е както транзитивна, така и симетрична. За да се получат що-годе адекватни семантики за тези два вида модални логики със сигурност трябват още формални свойства, но ще спрем дотук.
Ще завършим темата за модалните логики с някои по-философски въпроса, засягащи алетичната модалност (понятията за необходимост и възможност).
Различни видове необходимост и възможност
Алетичната модална логика (модалната логика в тесен смисъл) интерпретира силния и слабия модален оператор съответно като „необходимо“ и „възможно“. Необходимостта и възможността обаче могат да се разбират различно. Например, бихме могли да разграничим (без да претендираме за изчерпателност) логически, физически и контекстуален смисъл на понятията за необходимост и възможност. Твърдението „Възможно е да има тяло, което се движи със скорост, по-висока от скоростта на светлината“, е истинно, ако „възможно“ се разбира като логически възможно, но е неистинно, ако се разбира като физически възможно.
За семантиката на алетичната модална логика бихме могли да използваме семантичното правило (1), в което не се говори за релацията на достижимост. Често се приема, че получената по този начин семантика до голяма степен отговаря на интуитивното разбиране за „необходимо“ и „възможно“. Разликата между различните понятия за необходимост и възможност тогава ще се прояви като разлика между множествата от възможни светове W.
Когато необходимостта и възможността се схващат като логическа необходимост и възможност, W трябва да включва в себе си всички логически възможни светове. Тъй като е логически възможно физическите закони да са различни от тези, които са в действителност, и в частност е възможно да са такива, че да позволяват движение с по-висока скорост от скоростта на светлината, в W трябва да има възможни светове, в които има тела, които се движат с по-висока скорост от скоростта на светлината. В тези светове изречението „Има тяло, което се движи с по-висока скорост от скоростта на светлината“ ще е истинно, което по семантичното правило (1) ще направи изречението „Възможно е да има тяло, което се движи с по-висока скорост от скоростта на светлината“ истинно във всеки от възможните светове в W и значи и в нашия възможен свят.
Ако разбираме „необходимо“ и „възможно“ като физически необходимо и възможно, W би трябвало да бъде множеството на всички физически възможни светове, т.е. на тези, в които важат физическите закони на нашия свят, въпреки че много от световете ще бъдат твърде различни от нашия – например в някой от тях Земята и хората няма да съществуват и т.н. Множеството на всички физически възможни светове е правилно подмножество на множеството на всички логически възможни светове, тъй като физически възможните светове са също и логически възможни, но в много от логически възможните светове не важат законите на физиката (или част от тях). В нито един физически възможен свят например няма тяло, което се движи с по-висока скорост от скоростта на светлината. Поради това сред възможните светове в W няма да има свят, в който изречението „Има тяло, което се движи с по-висока скорост от скоростта на светлината“ е истинно, което съгласно семантичното правило (1) ще направи изречението „Възможно е да има тяло, което се движи с по-висока скорост от скоростта на светлината“ неистинно във всеки от световете в W, включително и в нашия възможен свят. Така това твърдение става неистинно, ако „възможно“ се разбира като физически възможно. От това, че физически възможните светове са правилно подмножество на логически възможните, следва, че всичко физически възможно е и логически възможно, но не и обратното – има неща, които са логически възможни, но физически невъзможни. По същата причина и всичко, което е логически необходимо, е и физически необходимо, но не и обратното – има неща, които са физически, но не и логически необходими.
Така както физическата необходимост е по-слаба от логическата, контекстуалната необходимост е по-слаба от физическата. Под „контекстуална необходимост и възможност“ ще разбираме разнообразните начини, по които „необходимо“ и „възможно“ се употребяват във всекидневния език. Ако например в някакъв контекст на обяд кажа на някого „Няма да ми е възможно да отида довечера на срещата“, аз имам предвид някакво множество от различни възможни развития на ситуацията от обяд до вечерта, зависещи и от моите действия и решения, но не само от тях. Правя това твърдение, защото преценявам, че при нито едно от тези възможни развития няма да е факт, че довечера ще отида на срещата. На всяко от възможните развития отговаря множество от физически възможни светове – освен ако не вярва в чудеса, човек приема, че всяко възможно развитие на ситуацията се осъществява в съответствие с физическите закони. По време на изказването на твърдението аз все още не зная какъв възможен свят ще се окаже в крайна сметка действителен, но тъй като (според мен) в нито един от възможните светове няма да е истинно твърдението „Довечера ще отида на срещата“, във всеки от тях ще е истинно твърдението „Няма да ми е възможно да отида довечера на срещата“ и значи това твърдение ще е истинно и в действителния свят. Така че можем да приемем, че в подобни ситуации множеството от възможните светове W се състои от физически възможни светове, всеки от които съдържа една от визираните от говорещия възможни развития на ситуацията от обяд до вечерта. (На едно възможно развитие на ситуацията отговарят много светове, защото те могат да се различават по най-различни ирелевантни детайли, като например, че в единия температурата довечера ще е 20, а в другия – 21 градуса и т.н.) Както множеството от физически възможните светове е правилно подмножество на множеството от логически възможните светове, така в различните ситуации множествата от контекстуално възможни светове са правилни подмножества на множеството от физически възможните светове. Това, че не всички физически възможни светове се взимат предвид в горната ситуация, е ясно от това, че в някои от тях Слънцето, Земята, аз и въпросната среща изобщо не съществуват.
Контра-фактуални условни изречения. Термини за предразположение
Така наречените контра-фактуални условни изречения (counterfactual conditionals) могат да бъдат анализирани логически посредством контекстуалната необходимост и възможност. Пример за такова изречение е „Ако Нютон не беше открил закона за всеобщото привличане, някой друг щеше да го открие“.
Да разгледаме следното негово (полу-)символно представяне:
| (3) | □ (Нютон не е открил закона за всеобщото привличане → Някой друг е открил закона за всеобщото привличане) |
В термините на семантиката на възможните светове (3) ни казва, че във всеки възможен свят от W (нека мислим за W като съдържащо всеки възможен вариант на развитие на човешката история) е истинно, че ако Нютон не е открил закона за всеобщото привличане, някой друг го е открил. С други думи във всяко възможно развитие или Нютон, или някой друг открива този закон. Това изглежда съответства на значението на началното изречение, така че бихме могли да приемем, че всяко изречение от вида „Ако се беше случило A, щеше да се случи B“ може да се представи символно с „□(α→β)“, където α и β са съответните символни представяния на изреченията A и B, а множеството от възможните светове W е такова, че съдържа всички релевантни алтернативни развития на историята според изказващия изречението. Подобно на примера с твърдението „Няма да ми е възможно да дойда довечера на срещата“ всички светове в W са физически възможни, но не е необходимо в него да се съдържат всички физически възможни светове. Спокойно можем например да си позволим физически възможните светове, в които Земята и хората не съществуват, да не са част от W. Така че, както изглежда, налице е понятието за контекстуална необходимост.
Нека обърнем внимание, че контра-фактуалните условни изречения не могат да бъдат третирани като прости материални импликации, т.е. като немодални изречения. Причината е, че всяка импликация „A→B“ е истинна, когато антецедентът ѝ A e неистинен, а в контра-фактуалните условни твърдения това се предпоставя – ние знаем, че Нютон е открил закона за всеобщото привличане, но говорим за фактически неистинния (но възможен) случай, ако не го беше открил. Ако не сложим силния модален оператор □ пред импликацията, всяко контра-фактуално условно твърдение, колкото и очевидно невярно да е, би се оказало тривиално истинно.
Използване на модалности изисква и логическият анализ на така наречените термини за предразположение (disposition terms) – предикати като „разтворим във вода“, „чуплив“, „страхлив“ и пр. Между тях и контра-фактуалните условни твърдения има връзка. Това, че нещо е разтворимо във вода, не значи нито че е разтворено във вода, нито че ще бъде разтворено във вода. То би могло да е такова дори ако вода не съществуваше. Разтворимостта във вода на нещо означава, че ако то беше потопено във вода, щеше да се разтвори. Изразено в термините на семантиката на възможните светове, това означава, че във всеки физически възможен свят, в който това нещо е потопено във вода, то се е разтворило в нея. Следователно изречението „a е разтворимо във вода“ може да се представи (полу-) символно по следния начин:
| □ (a е потопено във вода → a се е разтворило) |
Предикатът (терминът за предразположение) „…е разтворимo във вода“ следователно всъщност е следният съставен предикат, в който участват обикновени предикати и модален оператор:
| □ (…е потопено във вода → …се е разтворило) |
Ако представим предиката „…е потопено във вода“ с „F“ и „…се разтваря“ – с „G“, изцяло символното представяне на изречението „a е разтворимо във вода“ би било „□(Fa→Ga)“, а на съдържащият се в него предикат (термин за предразположение) „…е разтворимо във вода“ – „□(F…→G…)“. Силният модален оператор в случая изразява физическа необходимост.
Задачи
(Изтеглете задачите като pdf.)| (1) Представете символно следните изречения, като използвате символния езика на модалната пропозиционална логика. |
| 1) | Не е необходимо Иван да дойде на срещата. |
| 2) | По необходимост всичко е крайно или безкрайно. |
| 3) | Ако е задължително да участваш в изборите, значи това ти е и позволено. |
| 4) | Пушенето е забранено в стаята, но е позволено в коридора. |
| 5) | Това не само е възможно, то е възможно по необходимост. |
| 6) | Това е необходимо, но не е необходимо по необходимост. |
| 7) | Ако това се е случвало някога, то ще се случи и в бъдеще. |
| 8) | Възможно е всичко да е крайно по необходимост. |
| 9) | Не е необходимо това да е необходимо, но то е възможно по необходимост. |
| 10) | Ако това е позволено да е задължително, то е задължително да е позволено. |
| 11) | Ако това се случи някога, винаги е било факт, че ще се случи. |
| 12) | Ако това се е случвало някога, винаги ще е факт, че се е случвало. |
| 13) | Ако това е необходимо, то е факт, а ако е факт, значи е и възможно. |
| 14) | Ако винаги е било факт, че това е щяло да се случи, то ще дойде момент, в който вече се е случило. |
| 15) | Това се е случвало, но е имало момент, в който не се е случвало. |
| (2) Следните двойки изрази би трябвало да са логически еквивалентни по връзката между модалните оператори. Наистина ли е така? Ако не е, променете един от модалните оператори в първия израз, така че да станат логически еквивалентни? |
| 1) | ¬□α ◊¬α |
| 2) | ¬◊¬α ¬¬□α |
| 3) | □¬□□¬α ¬◊□¬□α |
| 4) | □¬¬◊¬α ¬◊□α |
| 5) | □¬□□¬α □◊◊α |
| 6) | ¬◊□□α □◊□¬α |
| 7) | ◊◊¬□□¬α ◊◊◊◊α |
| 8) | ◊◊¬□□¬α ¬□□□¬□α |
| 9) | ◊◊¬□□¬α ◊◊◊¬◊¬α |
| 10) | ◊◊□□¬α ¬□□□◊α |
| (3) Докажете с диаграми, че следните изрази са логически валидни по отношение на семантичното правило (1). |
| 1) | □α → ◊α |
| 2) | ◊□α → ◊α |
| 3) | [□(α→β) ∧ □¬β] → ¬α |
| 4) | (◊α ∧ ◊β) → ◊(α ∨ β) |
| 5) | [□(α ∨ β) ∧ □¬α] → □β |
| 6) | ◊(α ∨ β) → (◊α ∨ ◊β) |
| 7) | □α → □□□□α |
| 8) | ◊(α ∨ β) → (◊◊α ∨ ◊β) |
| 9) | [□(α ∨ β) ∧ □(α→γ) ∧ □(β→γ)] → □γ |
| 10) | ¬◊(α ∨ β) → □(¬α→ ¬β) |
| (4) Докажете с диаграми, че следните изрази са логически валидни (по отношение на семантичното правило (2), без да се предявяват изисквания към релацията на достижимост: |
| 1) | □(α→β) → (□α→□β) |
| 2) | (□α ∧ □β) → □(α ∧ β) |
| 3) | □α → □(α ∨ β) |
| 4) | (□α ∧ ◊β) → ◊(α ∧ β) |
| 5) | □(β→α) → ¬◊(¬α ∧ β) |
| 6) | □(α→β) → (◊α→◊β) |
| 7) | □□α → □(◊α ∨ □β) |
| (5) Докажете с диаграми, че следните изрази са логически валидни, когато релацията на достижимост е рефлексивна: |
| 1) | α → ◊α |
| 2) | □α → ◊◊α |
| 3) | □(□α→α) |
| 4) | □(α→◊α) |
| 5) | □□□α → α |
| 6) | □(α→β) → (α→◊β) |
| 7) | [□(¬α→β) ∧ (α→□β)] → ◊β |
| (6) Докажете с диаграми, че следните изрази са логически валидни, когато релацията на достижимост е транзитивна: |
| 1) | ◊◊α → ◊α |
| 2) | ◊◊◊α → ◊α |
| 3) | □α → □¬◊◊¬α |
| 4) | [◊◊◊(α→β) ∧ □α] → ◊β |
| 5) | □(α→β) → □(□α→□β) |
| 6) | □◊α → □◊□◊α |
| (7) Докажете с диаграми, че следните изрази са логически валидни, когато релацията на достижимост е симетрична: |
| 1) | ◊□α → α |
| 2) | ◊□α → □◊α |
| (8) Докажете с диаграми, че следните изрази са логически валидни, когато релацията на достижимост е симетрична и транзитивна: |
| 1) | ◊□α → □α |
| 2) | □(□α ∨ β) → (□α ∨ □β) |
| 3) | ◊□α → □□α |
| (9) Докажете с диаграми, че следните изрази са логически валидни, когато релацията на достижимост е рефлексивна и транзитивна: |
| 1) | ◊◊□α → ◊α |
| 2) | (□α ∨ □□□β) → (□□□α ∨ □β)5 |
1. „Aletheia“ значи „истина“ на старогръцки. ↩ 2. В темпоралната модална логика вместо „□α“ имаме „□pα“ и „□fα“, а вместо „◊α“ – „◊pα“ и „◊fα“, т.е. трябва да добавим четири вместо две правила. ↩ 3. Всички използвани схеми за извод и схеми еквивалентности са от 1.8 Естествена дедукция. ↩ 4. Едно множество е правилно подмножество на друго, когато всички елементи на първото са елементи на второто, но второто има елементи, които не са елементи на първото. ↩ 5. Решението изисква разглеждане на различни случаи. ↩

