2.4 Силогизми
Какво е силогизъм?
В традиционната логика се прави разлика между непосредствени изводи (които имат само една предпоставка) и „опосредствани“ изводи (които имат повече от една). В предишната секция разгледахме непосредствените изводи – подчиненост, обръщане, превръщане и контрапозиция. От опосредстваните изводи най-основни и важни са силогизмите. Ето два примера:
| (1) | Нито един метал не е изолатор. |
| Някои метали са течности. | |
| Някои течности не са изолатори. | |
| (2) | Всички хора са смъртни. |
| Нито един смъртен не е бог. | |
| Нито един бог не е човек. |
Всеки силогизъм се състои от две предпоставки и заключение. Освен това в него участват общо три термина (в (1) това са „течност“, „изолатор“ и „метал“, а в (2) – „бог“, „човек“ и „смъртен“). Субектът на заключението („течност“ в (1) и „бог“ – в (2)) се нарича „малък термин“ и освен в заключението участва в една от предпоставките (втората в примерите). Предикатът на заключението („изолатор“ в (1) и „човек“ в (2)) се нарича „голям термин“ и освен в заключението участва в другата предпоставка (първата в примерите). Малкият и големият термин се наричат още „крайни термини“. Третият от термините, който не участва в заключението, но участва и в двете предпоставки („метал“ в (1) и „смъртен“ в (2)), се нарича „среден термин“.
Предпоставката, която съдържа малкия термин (субекта на заключението), се нарича малка предпоставка, а тази, която съдържа големия термин (предиката на заключението), се нарича голяма предпоставка. И в двата примера голямата предпоставка е дадена първа, малката втора (и накрая е заключението) . Това е стандартният начин, по който ще подреждаме предпоставките в един силогизъм, когато искаме да го анализираме логически – първо голямата, после малката и накрая заключението. Когато този ред е спазен, ще казваме, че силогизмът е в стандартна форма. Стандартната форма е важна за единствено за целите на логиката (за правилния анализ на формата на един силогизъм). Тъй като по принцип редът на предпоставките е ирелевантен за валидността на изводите, не можем да очакваме, че винаги (или преобладаващо) ще срещаме силогизми в стандартна форма. Напротив, съвсем допустимо е някой да направи същите изводи като (1) или (2), като изкаже предпоставките в обратен ред (първо малката, после голямата) или дори като изкаже заключението преди предпоставките. Съвсем възможно и допустимо е да се каже „Някои течности не са изолатори, защото някои метали са течности, а нито един метал не е изолатор“. Това е валиден силогизъм, формулиран обаче не в стандартна форма – първо е изказано заключението, после малката и накрая голямата предпоставка (точно обратния на стандартното подреждане ред).
За да определим елементите на един силогизъм (кой е малкият термин, голямата предпоставка и т.н.) тръгваме от заключението. Субектът и предикатът на заключението са съответно малкият и големият термин. След като сме определили кой е малкият и кой – големият термин, можем да определим коя е голямата и коя е малката предпоставка – предпоставката, която съдържа малкия термин, е малката предпоставка, а тази, която съдържа големия термин – голямата. Средният термин е този, който се среща и в двете предпоставки и не се среща в заключението. След това за целите на логическия анализ е препоръчително да напишем силогизма в стандартна форма, т.е. да напишем първо голямата предпоставка, после малката и накрая заключението. Това е ключово за правилното определяне на фигурата и модуса на анализирания силогизъм.
Фигури на силогизма
Като правило малкият термин на един силогизъм се представя символно с „S“, големият – с „Р“, а средният – с „М“. Например, стандартното символно представяне на (1) и (2) е следното:
| (3) | MeP | PaM | |
| MiS | MeS | ||
| SoP | SeP |
От него ясно се вижда, че освен по вида на предпоставките и заключението, двата силогизма се различават по разположението на средния термин. В първия от тях средният термин (М) е субект и в двете предпоставки, а във втория е предикат в голямата и субект в малката. Разположението на средния термин определя фигурата на един силогизъм. Има четири възможни разположения на средния термин, които определят четирите фигури на силогизма:
| I фиг. | M – P | II фиг. | P – M | III фиг. | M – P | IV фиг. | P – M |
| S – M | S – M | M – S | M – S | ||||
| S – P | S – P | S – P | S – P |
В първа фигура средният термин (М) е субект в голямата и предикат в малката предпоставка. Във втора фигура е предикат и в двете предпоставки. В трета фигура е субект и в двете предпоставки. В четвърта фигура е предикат в голямата и субект в малката предпоставка.
От силогизмите (1) и (2), които представихме символно в (3), първият е от трета, а вторият – от четвърта фигура.
Модуси на силогизма
Освен по това, какви термини участват в тях, и коя е фигурата им, два силогизма могат да се различават и по вида на твърденията (двете предпоставки и заключението) – дали са А, E, I или О-твърдения. Видът на твърденията определя модуса на силогизма. Например в (1) голямата предпоставка е Е-твърдение, малката – I-твърдение, а заключението – О-твърдение, поради което той е от модус EIO, докато в (2) голямата предпоставка е А-твърдение, а малката предпоставка и заключението – Е-твърдения, поради което той е от модус АЕЕ (редът на буквите отговаря съответно на вида на голямата предпоставка, на малката предпоставка и на заключението). Логическата форма на един силогизъм е напълно определена от модуса и фигурата му. Така (1) е модус ЕIO от трета фигура, което ще записваме „EIO-3“, а (2) е модус АЕЕ от четвърта фигура (АЕЕ-4).
Тъй като в качеството му на схема за извод един силогизъм е напълно определен от модуса и фигурата, за да определим колко са всички възможни силогизми, трябва да определим колко са възможните комбинации от модуси и фигури. Възможните модуси са 64, защото за голямата предпоставка имаме 4 възможности (А, Е, I, или О ), които като се комбинират с още 4 възможности за малката предпоставка, се получават 4х4=16 възможности, които като се комбинират с още 4 възможности за заключението, се получават общо 16х4=64 възможни модуса. (EIO и АЕЕ модусите на двата наши примера са две от тези 64 възможности.) Тъй като освен това всеки един модус може да е в една от четирите фигури, като умножим броя на модусите с броя на фигурите, за общия брой на всички силогизми се получава 64x4=256.
От всички 256 силогизма само 24 са логически валидни, т.е. само при 24 от тях заключението следва логически от предпоставките.
Валидни силогизми
Двата наши примера, които представихме символно в (3) (EIO-3 и АЕЕ-4), са логически валидни. Валидността на АЕЕ-4 може да се види от следната диаграма:
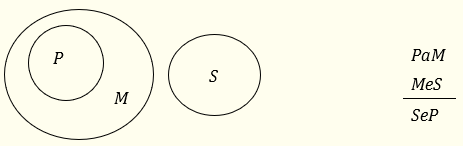
В голямата предпоставка се твърди, че всички Р са М, и значи обемът на Р е подмножество на обема на М. В малката предпоставка се твърди, че нито едно М не е S, и значи обемът на М няма общи елементи с този на S. Всички това е представено на диаграмата с кръгове. От нея се вижда, че обемите на S и Р не могат да имат обща част – щом като Р се включва напълно в М, а М се изключва напълно от S, то трябва и S да се изключва напълно от Р, т.е. по необходимост нито едно S не е Р, каквото се твърди в заключението.
Нека да разгледаме и един невалиден силогизъм, например ААА-4:
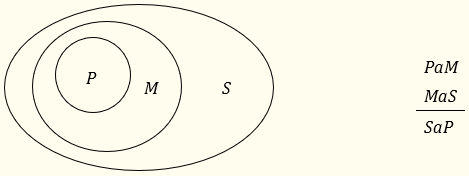
В голямата предпоставка се твърди, че всички Р са М, което е представено от отношението на двата най-вътрешни кръга. Във малката предпоставка се твърди, че всички М са S, на което в диаграмата отговаря това, че кръгът на М влиза напълно в кръга на S. В заключението се твърди, че всяко S е Р, но от диаграмата се вижда, че това е изпълнено само когато обемите на Р, М и S съвпадат. Когато това не е така (което впрочем е състоянието на нещата, показвано на диаграмата), има неща, които са S, но не са Р, и съответно заключението е неистинно, въпреки че предпоставките са истинни – следователно силогизмът е невалиден.
По-горе казахме, че от всичките 256 силогизма само 24 са валидни. Таблицата отдолу показва кои са те във всяка от четирите фигури:
| I фигура | II фигура | III фигура | IV фигура |
| AAA-1 (Barbara) | EAE-2 | AAI-3 | AAI-4 |
| ЕАЕ-1 (Celarent) | AEE-2 | IAI-3 | AEE-4 |
| AII-1 (Darii) | EIO-2 | AII-3 | EAO-4 |
| EIO-1 (Ferio) | AOO-2 | EAO-3 | IAI-4 |
| (AAI-1) | (EAO-2) | EIO-3 | EIO-4 |
| (EAO-1) | (AEO-2) | OAO-3 | (AEO-4) |
Във всяка фигура има по 6 валидни силогизма. Два от I-ва и II-ра фигура и един от IV-та са заградени в скоби. Тези силогизми имат същите предпоставки като други валидни силогизми от същата фигура, но за разлика от тях имат частно, а не общо заключение. Например в I-ва фигура AAI-1 има същите предпоставки (две А-твърдения) като AAA-1, но частно-утвърдително (I), а не общо-утвърдително (А) заключение. Същото важи и за EAO-1 и ЕАЕ-1 – предпоставките на двата силогизма са същите, но заключението на EAO-1 е частно-отрицателно, а на ЕАЕ-1 – общо-отрицателно. Както знаем от логическия квадрат, от всяко общо-утвърдително твърдение следва частно-утвърдително (със същия субект и предикат)1 и по същия начин от всяко общо-отрицателно следва частно-отрицателно. Поради това дадените в скоби силогизми с частно заключение са всъщност отслабени форми на силогизмите със същите предпоставки, но с общо заключение. От това, че всички хора са смъртни и всички гърци са хора, по AAA-1 може да се заключи, че всички гърци са смъртни. Но, разбира се, щом всички гърци са смъртни, то и някои (поне един) гърци ще са смъртни, т.е. от същите предпоставки ще следва не само твърдението „Всички гърци са смъртни“, но и по-слабото твърдение „Някои гърци са смъртни“. Това, че от същите предпоставки следва по-силно твърдение, до голяма степен обезсмисля тези отслабени форми на валидни силогизми. Като се абстрахираме от тях, валидните силогизми стават 19 – по четири в първа и втора фигура, шест в трета и пет в четвърта. По-нататък, когато говорим за валидни силогизми, ще имаме предвид тези 19 силогизма.
В таблицата с валидните силогизми по-горе след силогизмите от първа фигура в скоби са написани техните собствени имена. Тези имена са им дадени от средновековните логици и гласните в тях отговарят на модуса. Например трите „а“-та в „Barbara“ отговарят на трите А-твърдения в ААА-1. Всички валидни силогизми имат такива собствени имена. Посочили сме само тези на силогизмите от първа фигура, защото на последните в традиционната логика е придавано най-голямо значение. Причината за това е, че Аристотел ги предпоставя в качеството им на аксиоми и (в Първа аналитика) чрез тях доказва валидността на силогизмите от останалите фигури2. Важността на първа фигура идва освен това от факта, че от нея е единственият силогизъм с общо-утвърдително заключение (Barbara) – заключенията на валидните силогизми от втора фигура са само отрицателни, на тези от трета фигура – само частни, а на тези от четвърта са разнообразни, но липсва общо-утвърдително.
Преди да видим как посредством валидните силогизми от първа фигура Аристотел извежда валидността на силогизмите от останалите три фигури, нека се убедим интуитивно с диаграми в логическата валидността на Barbara, Celarent, Darii и Ferio (четирите валидни силогизма от първа фигура).

В предпоставките на Barbara се твърди, че всяко М е Р и че всяко S е М. Щом М-овете влизат напълно в Р-тата, а S-овете – в М-овете, то няма как S-овете да не влизат напълно в Р-тата, т.е. няма как всяко S да не е Р.
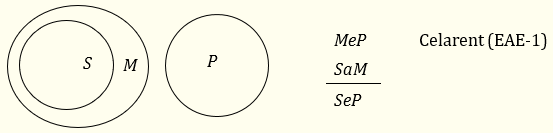
В предпоставките на Celarent се твърди, че всяко S е М и че нито едно М не е Р. Щом S-овете се включват в М-овете, а М-овете се изключват от Р-тата, то няма как S-овете да не се изключват от М-овете, т.е. по необходимост трябва нито едно S да не е Р.

В предпоставките на Darii се твърди, че всички М са Р и че някои S са M. Щом М се включва напълно в Р, а някаква част от S се включва в М, то тази същата част на S ще се включва в Р, т.е. някои S ще бъдат Р. (Това, че само някаква част от обема на S се включва в обема на М, на диаграмата е изобразено чрез това, че в кръга на М е начертана само част от кръга на S.)

В предпоставките на Ferio се твърди, че нито едно М не е Р и че някои S са М. Щом целият обем на М се изключва от обема на Р, а някаква част от обема на S се включва в обема на М, то същата тази част от обема на S ще се изключва от обема на Р, т.е. някои S няма да са Р, което се твърди в заключението.
Нека видим сега как Аристотел доказва валидността на валидните силогизми от другите три фигури посредством валидността на Barbara, Celarent, Darii и Ferio, в която се убедихме интуитивно чрез диаграми. Доказателствата използват операцията обръщане и това, че двойките твърдения А и О, от една страна, и Е и I, от друга, са точни отрицания едно на друго (виж логическия квадрат).
Като първи пример нека докажем валидността на ЕАЕ-2:
| РeМ |
| SаM |
| SеP |
Приемаме, че предпоставките са истинни и искаме да докажем, че от тях следва заключението:
| 1. РeМ |
| 2. SaM / SеP |
От 1. по операцията обръщане следва MeP:
| 3. MeP от 1. по обръщане |
Сега от 3. и 2. можем да изведем SeP (това което търсим) въз основа на валидния силогизъм от първа фигура EAE-1 (Celarent), в който 3. играе ролята на голяма, а 2. – на малка предпоставка:
| МеР |
| SаM |
| SеP |
| 4. SeP от 3. и 2. по Celarent |
Като следващ пример ще докажем валидността на АЕЕ-4 (втория пример в (3) по-горе):
| 1. PaM |
| 2. MeS / SeP |
| 3. PeS от 2. и 1. по Celarent |
| 4. SeP от 3. по обръщане |
При извода на 3. от 2. и 1. с използване на Celarent голямата предпоставка в последния е MeS (2.), a малката е РаМ (1.). P играе ролята на малък термин, M – на среден, а S – на голям, т.е. имаме следното:
| MeS |
| РаМ |
| РeS |
Не всички валидни силогизми от останалите три фигури могат да се изведат директно от четирите валидни силогизма на първа фигура с използване на операцията обръщане. Пример на силогизъм, за който това не е възможно е АОО-2:
| РаМ |
| SoM |
| SoP |
Както знаем, частно-отрицателното (О) твърдение не може да се обръща. Следователно при доказателството на този силогизъм можем да обърнем само голямата предпоставка „РаМ“, в резултат на което ще получим „MiP“. Тогава заедно с „SoM“ ще имаме на разположение две частни твърдения. Но в първа фигура няма валиден силогизъм с две частни предпоставки – всъщност изобщо не съществува такъв валиден силогизъм. Следователно тук не може да подхождаме както досега. В случаи като този, където не е възможно директно доказателство, Аристотел използва доказателство чрез свеждане до противоречие. Да видим как става това с въпросния АОО-2:
| 1. PaM |
| 2. SoM / SoP |
| 3. SaP (¬SoP) допускане |
| 4. SaM от 1. и 3. по Barbara (S – малък, Р – среден, М –голям термин) – противоречие с 2. |
| 5. SoP от 3. – 4. по свеждане до противоречие |
В 3. сме допуснали отрицанието на заключението („¬SoP“). Тъй като обаче А и О-твърденията са точни отрицания едно на друго, всъщност сме допуснали „SaP“. По същата причина 4. („SaM“) противоречи на 2. („SoM“).
Всеки валиден силогизъм от останалите три фигури (дадени в таблицата по-горе) може да се изведе по един от двата показани начина – с директно доказателство или с доказателство чрез свеждане до противоречие.
Освен това не е необходимо да приемаме като аксиоми и четирите валидни модуса от първа фигура. Ако приемем като аксиома само Barbara и който и да е от другите три, с доказателство чрез свеждане до противоречие можем да изведем останалите два. Например, ако приемем като аксиоми Barbara и Celarent, Darii и Ferio се извеждат по следния начин:
| 1. MaP |
| 2. SiM / SiP |
| 3. SeP (¬SiP) допускане |
| 4. PeS от 3. по обръщане |
| 5. MeS от 4. и 1. по Celarent (М – малък, Р – среден, S – голям термин) |
| 6. SeM от 5. по обръщане – противоречие с 2. |
| 7. SiP от 3. – 6. по свеждане до противоречие |
| 1. MeP |
| 2. SiM / SoP |
| 3. SaP (¬SoP) допускане |
| 4. PeM от 1. по обръщане |
| 5. SeM от 4. и 3. по Celarent (S – малък, Р – среден, M – голям термин) – противоречие с 2. |
| 6. SoP от 3. – 5. по свеждане до противоречие |
Задачи
(Изтеглете задачите като pdf.)| (1) Долните аргументи са силогизми. За всеки от тях определете кой е малкият, големият и средният термин в него и кои са голямата и малката предпоставка? Преформулирайте го в стандартна форма и го представете символно. Определете модуса и фигурата. |
| 1) | Някои космически тела се движат по елиптични орбити, защото всички планети са космически тела и всички планети се движат по елиптични орбити. |
| 2) | Всички патици имат два крака и понеже Сократ има два крака, значи е патица. |
| 3) | Някои богати хора са амбициозни. Следователно, доколкото всички банкери са богати, някои амбициозни хора са банкери. |
| 4) | Онтологическо доказателство: Бог съществува, защото всяко напълно съвършено нещо съществува, а Бог е напълно съвършен. |
| 5) | Всички животни са организми и всички птици са животни. От това следва, че някои организми са птици. |
| 6) | Нито един престъпник не е благороден човек, защото всеки благороден човек уважава закона, докато никой престъпник не го уважава. |
| 7) | Всички поети са деликатни хора, но някои от тях са войници. Следователно някои войници са деликатни хора. |
| 8) | Всички птици могат да летят и понеже някои домашни животни не са птици, значи някои домашни животни не могат да летят. |
| 9) | Никое деспотично управление не води до прогрес. Следователно, тъй като всяка добра форма на управление води до прогрес, нито една добра форма на управление не е деспотична. |
| 10) | Всички протеини са органични съединения. Така че, доколкото всички ензими са органични съединения, всички ензими са протеини. |
| (2) Като използвате валидните силогизми от първа фигура и операцията обръщане, докажете, че следните силогизми са валидни. |
| 1) | EIO-2 |
| 2) | AEE-2 |
| 3) | AII-3 |
| 4) | EAO-3 |
| 5) | OAO-3 |
| 6) | AAI-4 |
| 7) | EIO-4 |
1. За да е валидно това следване, необходимо е обемът на субекта да не е празно множество – нещо, което традиционната логика мълчаливо предпоставя. ↩ 2. По някаква причина Аристотел не се занимава с четвърта фигура, но силогизмите в нея се доказват съвсем аналогично по начина, чрез който доказва силогизмите от 2-ра и 3-та фигура. ↩

