2.3 Непосредствени изводи
Изводи с една предпоставка (и едно заключение) се наричат непосредствени в традиционната логика. Ще наричаме такива изводи операции.
- Подчинеността като непосредствен извод
В предишната секция видяхме, че според традиционната логика от общите твърдения логически следват техните подчинени, т.е. от едно общо-утвърдително или общо-отрицателно твърдение можем валидно да изведем съответно частно-утвърдителното или частно-отрицателното твърдение със същия субект и предикат. Два примера:
| Всички делфини са бозайници. | Нито един човек не е безгрешен. | |
| Някои делфини са бозайници. | Някои хора не са безгрешни. |
Символно:
| SaP | SeP | |
| SiP | SoP |
Това са непосредствени изводи, тъй като имат една предпоставка. Няма да разглеждаме другите отношения в логическия квадрат като непосредствени, тъй като те представляват преходи от истинността на едно твърдение към неистинността на друго, или обратно, а не от истинността на едно твърдение към истинността на друго.
Обръщане
Обръщането е извод, който има една предпоставка и в заключението му участват същите термини като в предпоставката, но разменени – субектът е станал предикат, а предикатът – субект. Ето един пример:
| Нито една котка не е земноводно. |
| Нито едно земноводно не е котка. |
Субект в предпоставката е терминът „котка“, а предикат – терминът „земноводно“. В заключението е обратно – „земноводно“ е предикат, а „котка“ – субект. Изводът е логически валиден. Когато са изпълнени условията изводът да е валиден и субектът и предикатът на предпоставката да са разменени в заключението, за твърдението на предпоставката казваме, че е подложено на операцията обръщане, в резултат на което е получено твърдението на заключението; накратко – твърдението на предпоставката се обръща в твърдението на заключението.
Общо-отрицателните (Е) твърдения се обръщат в общо-отрицателни твърдения:
| Нито едно S не е Р. | SeР | Пример: | Нито един метал не е изолатор. | |||
| Нито едно Р не е S. | РeS | Нито един изолатор не е метал. |
За да се убедим, че обръщането на Е-твърденията в Е-твърдения е логически валидно, нека разгледаме долната диаграма, която показва всички възможни отношения между обемите на субекта (S) и предиката (P) на едно категорично твърдение:
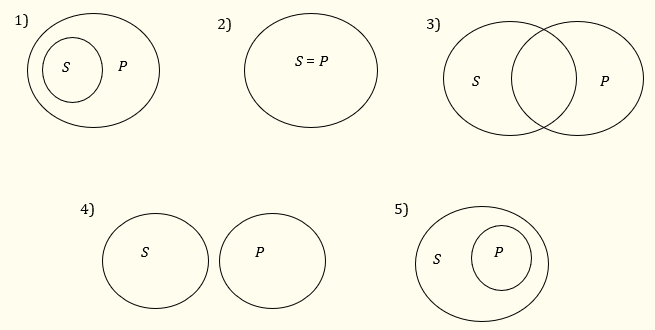
Единственият възможен случай, когато предпоставката „Нито едно S не е Р“ е истинна е 4). В този случай „Нито едно Р не е S“ също е истинно. Следователно, когато предпоставката е истинна, не е възможно заключението да е неистинно, което означава, че изводът е валиден.
От „Нито едно S не е P“ следва „Нито едно P не S“, но и от второто следва първото. Двете изречения са всъщност логически еквивалентни: имаме SeP ⟺ PeS (не само SeP ⇒ PeS).
Частно-утвърдителните (I) твърдения се обръщат в частно-утвърдителни:
| Някои S са Р. | SiР | Пример: | Някои камъни са прозрачни. | |||
| Някои Р са S. | РiS | Някои прозрачни неща са камъни. |
Можем да се убедим в логическата валидност на обръщането в този случай отново с горната диаграма. „Някои S са Р“ е истинно в случаи 1), 2), 3) и 5). Във всеки от тях е истинно и „Някои Р са S“.
Както при E-твърденията, тъй като “Някои S са P” и “Някои P са S” са симетрични, логическото следване е в двете посоки. Имаме SiP ⟺ PiS (не само SiP ⇒ PiS).
Общо-утвърдителните (А) твърдения се обръщат в частно-утвърдителни (I) твърдения:
| Всяко S е Р. | SaР | Пример: | Всяка котка е бозайник. | |||
| Някои Р са S. | РiS | Някои бозайници са котки. |
От “Всяко S е P” не може да се изведе “Всяко P е S”. Например, факт е, че всички дървета са растения, но не истинно, че всички растения са дървета. Проблемният случай е, когато обемът на S е строго подмножество на обема на P. Тогава „Всяко S e P“ е истинно, но „Всяко P е S“ е неистинно. В този случай обаче би могло да се изведе твърдението “Някои P са S”. Например, от “Всички дървета са растения” можем да изведем, че някои растения са дървета. В общия случай валидността на схемата за извод SaP ⇒ PiS може да се види от следното. От “Всяко S е P” (SaP) се извежда подчиненото му “Някои S са P” (SiP), а, както видяхме, от последното по обръщане следва твърдението “Някои P са S” (PiS).1
За разлика от Е и I твърденията, резултатът от обръщането на “Всяко S е P” не му е логически еквивалентен. От “Всяко S e P” следва “Някои P са S”, но от второто не следва първото. Например, от “Някои котки са животни” не следва “Всички животни са котки”.
При частно-отрицателните (О) твърдения операцията обръщане не е възможна, т.е. О-твърдението не може да се обърне валидно. От SoP не следва нито PaS, нито PеS, нито PiS, нито PоS. Това се вижда от следното. Предпоставката „Някои S не са Р“ е истинна в случаи 3), 4) и 5) на диаграмата. „Всяко Р е S“ (PaS) не е истинно в случаи 3) и 4). „Нито едно Р не е S“ (PеS) не е истинно в случаи 3) и 5). „Някои Р са S“ (PiS), не е истинно в случай 4). Най-силният кандидат, „Някои Р не са S“ (РоS), не е истинно в случай 5), когато обемът на P е строго подмножество на обема на S. В този случай има някакви S, които не са P, но всички P са S, което прави изречението “Някои P не са S” неистинно. Например, „Някои бозайници не са котки“ е истинно, но „Някои котки не са бозайници“ не е.
Долната таблица обобщава непосредствения извод на обръщането:
| Вид | Предпоставка | Заключение | Символно |
| A | Всяко S е P. | Някои P са S. | SaP ⇒ PiS |
| E | Нито едно S не е P. | Нито едно P не е S. | SeP ⟺ PeS |
| I | Някои S са P. | Някои P са S. | SiP ⟺ PiS |
| O | Някои S не са P. | (Не се обръща.) |
Превръщане
Освен за обръщане (и подчиненост) в традиционната логика се говори за още два вида непосредствени изводи: превръщане и контрапозиция. Те използват понятието за допълнение, затова нека накратко да се спрем на него.
- допълнение
Първичната употреба на това понятие се отнася до множествата. Множеството Y е допълнение на множеството X, ако съдържа точно тези неща, които Х не съдържа (само такива и всички такива неща). Например, ако X е множеството на всички котки, неговото допълнение е множеството на всички не-котки. Последното множество включва всички неща, които не са котки (включително всички неживи неща). Множеството на котките е обемът на термина „котка“, а допълнението на това множество е обемът на термина „не-котка“. Така, тръгвайки от произволен термин S, чийто обем е множеството X, винаги можем да образуваме друг термин, чийто обем е допълнението на X („котка“ – „не-котка“, „човек“ – „не-човек“ и т.н.). Затова, като вторично значение, ще отнасяме понятието за допълнение не само към множества, а също и към термини, образувани от други термини чрез добавяне на отрицателната частица „не“. Например, бихме могли да говорим за множеството на всички не-котки като допълнението на множеството на всички котки, но също бихме могли да говорим за термина „не-котка“ като допълнението на термина „котка“.
Забележете, че допълнението на допълнението на едно множество е самото множество – една не-не-котка е просто котка. Затова (обикновено) допълнението на допълнението на един термин може да се замества със самия термин.
Важно е допълнението на един термин да не се бърка с противния му термин. Допълнението на термина „красив“ не е термина „грозен“ (който е противния му термин), а е терминът „не-красив“. Освен неща, които са грозни, под последния термин попадат и неща, които са нито красиви, нито грозни. Ако един термин е допълнението на друг, то всяко едно нещо попада под единия или под другия термин. Можем да използваме това като тест за проверка дали един термин е допълнението на друг. Всяко нещо е котка или не-котка, но не всяко нещо красиво или грозно.
Преминаваме към непосредствения извод на превръщането (операцията превръщане). Ето един пример:
| Всички хора са смъртни. |
| Нито един човек не безсмъртен. |
За да подложим едно твърдение на операцията превръщане, заменяме предиката с неговото допълнение и променяме качеството му – от утвърдително на отрицателно, и обратно. В примера предикатът „смъртен“ е заменен с допълнението му „безсмъртен“ и видът на твърдението е сменен от общо-утвърдително на общо-отрицателно – количеството се запазва (общо твърдение), но качеството се променя от утвърдително на отрицателно.
За разлика от обръщането, превръщането е логически валиден извод и при четирите вида категорични твърдения. Освен това едно твърдение и неговото превърнато са винаги логически еквивалентни. Налице е логически следване и в двете посоки, защото заменянето на предиката с допълнението му и промяната на качеството на твърдението се неутрализират взаимно, така че се получава твърдение със същото значение. Нека видим как изглежда превръщането при всеки от четирите вида категорични твърдения.
Едно общо-утвърдително (А) твърдение „Всяко S е P“ се превръща в Е-твърдението „Нито едно S не е не-P“. Например, „Всички котки са интелигентни“ се превръща в „Нито една котка не е не-интелигентна“. За да се убедим в логическата валидност на схемата за извод SaP ⇒ S e не-P, отново можем да използваме горната диаграма. Предпоставката „Всяко S е P“ е истинна в случаи 1) и 2). Множеството на всички не-P е представено в диаграмата от цялата област извън кръга на P. И в двата въпросни случая няма застъпване между тази област и кръга на S, така че нито едно S не е не-P, когато всички S са P.
| Всяко S е P. | SaР | Пример: | Всички котки са интелигентни. | |||
| Нито едно S не е не-P. | S e не-P | Нито една котка не е не-интелигентна. |
Едно общо-отрицателно (Е) твърдение „Нито едно S не е P“ (SeP) се превръща в А-твърдението „Всяко S e не-P“ (S a не-P). Например, от „Нито една котка не е интелигентна“ можем валидно да изведем „Всяка котка е не-интелигентна“. „Нито едно S не е P“ е истинно в случай 4) на диаграмата. В този случай кръгът на S се включва напълно в областта извън кръга на P (съответстваш на множеството на всички не-P). Значи всички S са не-P, когато нито едно S не е P.
| Нито едно S не е P. | SeР | Пример: | Нито една котка не е интелигентна. | |||
| Всяко S е не-P. | S a не-P | Всяка котка е не-интелигентна. |
Едно частно-утвърдително (I) твърдение „Някои S са P“ (SiP) се превръща в О-твърдението „Някои S не са не-P“ (S o не-P). Например, „Някои котки са интелигентни“ се превръща в “Някои котки не са не-интелигентни“. Еквивалентността на двете твърдения е очевидна, като се вземе предвид, че множеството на нещата, които не са не-P, е точно множеството на нещата, които са P.
| Някои S са P. | SiР | Пример: | Някои котки са интелигентни. | |||
| Някои S не са не-P. | S o не-P | Някои котки не са не-интелигентни. |
Едно частно-отрицателно (0) твърдение „Някои S не са P“ (SoP) се превръща в I-твърдението „Някои S са не-P“ (S i не-P). Например, „Някои котки не са интелигентни“ се превръща в „Някои котки са не-интелигентни“. Еквивалентността на твърденията е дори по-очевидна от предишния случай.
| Някои S не са P. | SoР | Пример: | Някои котки не са интелигентни. | |||
| Някои S са не-P. | S i не-P | Някои котки са не-интелигентни. |
Във всеки от случаите показахме, че превърнатото на едно твърдение следва логически от него. Това, че всъщност твърденията са всъщност логически еквивалентни (че началното твърдение също следва от превърнатото), се вижда от факта, че превърнатото на превърнатото е началното твърдение. Например, като превърнем „Всяко S е P“ (SaP), получаваме „Нито едно S не е не-P“. Като отново превърнем последното твърдение, получаваме „Всяко S е не-не-P“, в което двете „не“-та могат да се махнат. Това показва, че „Всяко S е P“ следва логически от „Нито едно S не е не-P“ (превърнатото му) по превръщане (за което вече сме показали, че е валидно). Същото е налице и при останалите три вида категорични твърдения.
Долната таблица обобщава операцията превръщане:
| Вид | Предпоставка | Заключение | Символно |
| A | Всяко S е P. | Нито едно S не е не-P. | SaP ⟺ S e не-P |
| E | Нито едно S не е P. | Всяко S е не-P. | SeP ⟺ S a не-P |
| I | Някои S са P. | Някои S не са не-P. | SiP ⟺ S o не-P |
| O | Някои S не са P. | Някои S са не-P. | SoP ⟺ S i не-P |
Контрапозиция
Термини сменят местата си при обръщането или биват отричани при превръщането. При непосредствения извод на контрапозицията стават и двете неща – термини биват отричани и сменят местата си. Ето един пример:
| Всички наркотици предизвикват зависимост. |
| Нито една субстанция, която не предизвиква зависимост, не е наркотик. |
При контрапозицията допълнението на предиката става субект. На този непосредствен извод трябва да се гледа като получен чрез последователно прилагане на първо на превръщане и след това на обръщане:
| превръщане ⇨ обръщане |
Както видяхме, операцията превръщане е валидна винаги, но обръщането е невалидно при О-твърденията. Така че това валидността на контрапозицията ще зависи от втората стъпка на обръщането – ако то е валидно, и контрапозицията ще е валидна. Нека видим как ще изглежда контрапозицията при всеки от четирите типа категорични твърдения.
От едно общо-утвърдително (А) твърдение „Всяко S e P“ (SaP) при контрапозиция се получава логически еквивалентното твърдение „Нито едно не-P не е S“ (не-P e S). Например, от „Всички котки са интелигентни“ можем валидно да изведем „Нито едно не-интелигентно същество не е котка“. Това, че двете твърдения са логически еквивалентни, се вижда от факта, че второто се получава от първото както следва. Като подложим на превръщане „Всяко S е P“ („Всички котки са интелигентни“), получаваме „Нито едно S не е не-P“ („Нито една котка не е не-интелигентна“). Както знаем, резултатът от превръщането е винаги еквивалентно твърдение. След това, подлагайки на обръщане полученото твърдение, получаваме „Нито едно не-P не е S“ („Нито едно не-интелигентно същество не е котка“). По принцип, при обръщането не винаги се получава еквивалентно твърдение, но когато предпоставката е E-твърдение, това е така. Тъй като двете стъпки са еквивалентни преобразувания, всяко А-твърдение и резултатът от подлагането му на контрапозиция са еквивалентни (следват логически едно от друго).
| Всяко S е P. | SaР | Всички котки са интелигентни. | ||||
| Нито едно не-P не е S. | не-P e S | Нито едно не-интелигентно същество не е котка. |
От едно частно-отрицателно (О) твърдение „Някои S не са P“ (SoP) при контрапозиция се получава логически еквивалентното твърдение „Някои не-P са S“ (не-P i S). Например, от „Някои котки не са интелигентни“ можем валидно да изведем „Някои не-интелигентни същества са котки“. Валидността на извода е резултат от същата последователност от еквивалентни трансформации – превръщане и обръщане. „Някои S са P“ (SoP) се превръща в „Някои S са не-P“ (S i не-P), чието обръщане е еквивалентното му „Някои не-P са S“ (не-P i S).
| Някои S не са P. | SoР | Някои котки не са интелигентни. | ||||
| Някои не-P са S. | не-P i S | Някои не-интелигентни същества са котки. |
По контрапозиция от едно общо-отрицателно (E) твърдение „Нито едно S не е P“ се получава твърдение, което следва от него, но не му е еквивалентно, подобно на обръщането при А-твърденията. Това, че от „Нито едно S не е P“ не следва „Всички не-P са S“, може да се види с пример. „Нито една котка не е куче“ е истинно, но „Всички не-кучета са котки“ не е – хората например са не-кучета, които не са котки. Причината за невалидността на такъв извод е, че при първата стъпка на превръщането получаваме A-твърдение – „Всяко S е не-P“ („Всички котки са не-кучета“), което не може да се обърне в А-твърдение. От „Всички котки са не-кучета“ не следва „Всички не-кучета са котки“, а „Някои не-кучета са котки“. Поради това, полученото при превръщането твърдение може да се обърне единствено в „Някои не-P са S“. Резултатът е, че по контрапозиция от едно общо-отрицателно твърдение „Нито едно S не е P“ (SeP) можем да изведем „Някои не-P са S“ (не-P i S) – същото заключение като при контрапозицията на O-твърденията.
| Нито едно S не е P. | SeР | Нито една котка не е интелигентна. | ||||
| Някои не-P са S. | не-P i S | Някои не-интелигентни същества са котки. |
Контрапозицията е невалидна при частно-утвърдителните (I) твърдения. Причината е, че след превръщането на „Някои S са P“ се получава O-твърдението „Някои S не са не-P“, а, както знаем, при O-твърденията обръщането е невалидно. Например, приемайки че всяко нещо е идентично със себе си, ако тръгнем от истинното I-твърдение „Някои жени са идентични със себе си“ (SiP), след превръщането получаваме „Някои жени не са не-идентични със себе си“, което е същото като истинното твърдение „Някои жени не са различни от себе си“. Очевидно, последното не може да бъде обърнато в неистинното твърдение „Някои неща, които са различни от себе си, не са жени“. Твърдението е неистинно, тъй като няма неща които да са различни от (да не са идентични със) себе си.
Долната таблица обобщава непосредствения извод на контрапозицията:
| Вид | Предпоставка | Заключение | Символно |
| A | Всяко S е P. | Нито едно не-P не е S. | SaP ⟺ не-P e S |
| E | Нито едно S не е P. | Някои не-P са S. | SeP ⇒ не-P i S |
| I | Някои S са P. | (Няма валиден извод.) | |
| O | Някои S не са P. | Някои не-P са S. | SoP ⟺ не-P i S |
Бихме могли да използваме поредици от непосредствени изводи, за да доказваме, че (или да проверяваме дали) от дадено изречение логически следва друго – нещо, което може да не е очевидно. Използването на символните представяния вместо самите изречения значително улеснява намирането на такива доказателства, както и тяхното следване (проверка). Като пример ще покажем, че от твърдението „Всички социалисти са пацифисти“ логически следва твърдението „Някои не-социалисти не са пацифисти“.
Представяме символно предпоставката с SaP (S за „социалист“ и P за “пацифист”). Тогава заключението би трябвало да се представи с „не-S o P“. Ето едно доказателство за валидността на извода:
| 1. SaP / не-S o P |
| 2. S e не-P 1, превръщане |
| 3. не-P e S 2, обръщане |
| 4. не-P a не-S 3, превръщане |
| 5. не-S i не-P 4, обръщане |
| 6. не-S o не-не-P 5, превръщане |
| 7. не-S o P 6, махаме “не-не-” |
Задачи
(Изтеглете задачите като pdf.)| (1) Какво следва логически от всяко от следните твърдения по подчиненост, обръщане, превръщане и контрапозиция? |
| 1) | Всички тигри са бозайници. |
| 2) | Някои атлети не са професионалисти. |
| 3) | Нито един метал не е органично вещество. |
| 4) | Всички ловци на бисери са добри плувци. |
| 5) | Някои наркотици не предизвикват зависимост. |
| 6) | Някои хора, завършили университет, са шахматисти. |
| 7) | Нито един оптимист не е човек, който познава живота. |
| 8) | Някои активни противници на вдигането на корпоративния данък са членове на търговската камара. |
| (2) Докажете, че от твърдението „Всички социалисти са пацифисти“ логически следват следните твърдения. |
| 1) | Някои пацифисти не са не-социалисти. |
| 2) | Някои не-пацифисти не са социалисти. |
| (3) Докажете, че от твърдението „Нито един социалист не е пацифист“ следват логически следните твърдения. |
| 1) | Някои социалисти са не-пацифисти. |
| 2) | Някои пацифисти са не-социалисти. |
| 3) | Някои не-пацифисти са социалисти. |
| 4) | Някои не-социалисти не са не-пацифисти. |
1. Както обикновено, предпоставяме, че S не е празно. Иначе SaP ⇒ PiS няма да е валидна схема, защото липсата на S-ове прави SaP истинно, а PiS неистинно. Виж този параграф от предишната секция. ↩

